题目内容
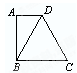
 如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )分析:根据等边三角形性质得出DB=DC=BC=8cm,∠DBC=60°,求出∠ABD=30°,求出AD=
BD=4cm,代入梯形ABCD的中位线
(AD+BC)求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵△DBC是等边三角形,
∴DB=DC=BC=8cm,∠DBC=60°,
∵∠ABC=90°,
∴∠ABD=30°,
∵∠A=90°,
∴AD=
BD=4cm,
∴梯形ABCD的中位线是
(AD+BC)=
×(4cm+8cm)=6cm,
故选B.
∴DB=DC=BC=8cm,∠DBC=60°,
∵∠ABC=90°,
∴∠ABD=30°,
∵∠A=90°,
∴AD=
| 1 |
| 2 |
∴梯形ABCD的中位线是
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了等边三角形性质,直角梯形,梯形的中位线的应用,关键是求出AD和BC的长.

练习册系列答案
相关题目
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为( )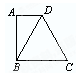
| A.4cm | B.6cm | C.8cm | D.10cm |