题目内容

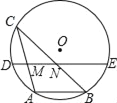
【题目】如图，⊙O的弦AB＝4cm，点C为优弧上的动点，且∠ACB＝30°．若弦DE经过弦AC、BC的中点M、N，则DM+EN的最大值是_____cm．

【答案】6．

【解析】

由点M、N分别是AC、BC的中点，根据三角形中位线定理得出MN=AB为定值，则NE+DM=DE-MN，所以当MN取最大值时，DM+EN有最大值．而直径是圆中最长的弦，故当DE为⊙O的直径时，可求得DM+EN的最大值．

当DE为⊙O的直径时，DM+EN有最大值；

当DE为直径时，M点与O点重合，

∴AC也是直径，AC=8cm，

∵∠ABC是直径所对的圆周角，

∴∠ABC=90°，

∵∠C=30°，AB=4cm，

∴AB=AC=8，

∵点M、N分别为AC、BC的中点，

∴MN=AB=2，

∴DM+EN=DE-MN=8-2=6，

故答案为：6．

练习册系列答案
相关题目

【题目】下图为某小区的两幢1O层住宅楼，由地面向上依次为第1层、第2层、…、第10层，每层的高度为3m，两楼间的距离AC=30m．现需了解在某一时段内，甲楼对乙楼的采光的影响情况．假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h，太阳光线与水平线的夹角为α．

(1)用含α的式子表示h；

(2)当α＝30°时，甲楼楼顶B的影子落在乙楼的第几层?从此时算起，若α每小时增加10°，几小时后，甲楼的影子刚好不影响乙楼采光．

【题目】（14分）如图，已知抛物线（）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．

（1）求此抛物线的解析式；

（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；

（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．

【题目】如图：已知△ABC中，AB＝5，BC＝3，AC＝4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．

（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；

（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；

（3）试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长．

【题目】已知二次函数y=﹣x2+4x+m．

（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；

（2）如图，二次函数的图象过点A（6，0），与y轴交于点B，点p是二次函数对称轴上的一个动点，当PB+PA的值最小时，求p的坐标

（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

（1）求证：ED为⊙O的切线；

（2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

试题解析：(1)证明：连接OD，

∵OE∥AB，

∴∠COE=∠CAD，∠EOD=∠ODA，

∵OA=OD,

∴∠OAD=∠ODA，

∴∠COE=∠DOE，

在△COE和△DOE中，

∴△COE≌△DOE(SAS)，

∴ED⊥OD，

∴ED是的切线；

(2)连接CD，交OE于M，

在Rt△ODE中，

∵OD=32，DE=2，

∵OE∥AB，

∴△COE∽△CAB，

∴AB=5，

∵AC是直径，

∵EF∥AB，

∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
25

【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

【题目】如图，四边形OABC是矩形，ADEF是正方形，点A，D在x轴的正半轴，点C在y轴的正半轴上，点F在AB上，点B，E是双曲线y1=与直线y2=mx+n的交点，OA＝2，OC＝6．

（1）求k的值；

（2）求正方形ADEF的边长；

（3）直接写出不等式>mx+n的解集．

【题目】如图，正方形ABCD中，AB=，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF.

(1)若A，E，O三点共线，求CF的长；

(2)求△CDF的面积的最小值.

【题目】如图，在平面直角坐标系xOy中，每个小正方形的边长都为1，和的顶点都在格点上，回答下列问题：

可以看作是经过若干次图形的变化平移、轴对称、旋转得到的，写出一种由得到的过程：______；

画出绕点B逆时针旋转的图形；

在中，点C所形成的路径的长度为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网