题目内容
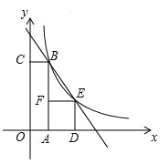
【题目】如图，四边形OABC是矩形，ADEF是正方形，点A，D在x轴的正半轴，点C在y轴的正半轴上，点F在AB上，点B，E是双曲线y1=
与直线y2=mx+n的交点，OA＝2，OC＝6．
（1）求k的值；
（2）求正方形ADEF的边长；
（3）直接写出不等式>mx+n的解集．
【答案】（1）k＝12；（2）
；（3）0<x<2或x>
【解析】
(1)根据OA＝2，OC＝6， 可得点B坐标为（2，6），代入反比例函数的解析式即可解答；（2）由（1）解得反比例函数解析式为y=
，设AD=t，则OD=2+t，所以E点坐标为（2+t，t），再根据反比例函数图象上点的坐标特征得（2+t）t=12，利用因式分解法可求出t的值；（3）反比例函数的函数值大于一次函数，即对应相同的x的值时，一反比例函数对应的点在一次函数的图象的点的上边，据此即可判断．
解：（1）∵OA＝2，OC＝6， ∴点B坐标为（2，6）
∴ 
，∴k＝12；
（2）设正方形边长为a，则点E坐标为（a+2，a），
∴a（a+2）＝12，解得：a＝
，
又a>0，∴a＝
；
（3）不等式
>mx+n的解集是：0<x<2或x>
练习册系列答案
相关题目
