题目内容
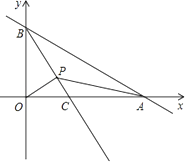
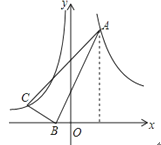
【题目】如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(-1,0),A点的横坐标是2,AB=3BC,双曲线![]() 经过A点,双曲线y=-
经过A点,双曲线y=-![]() 经过C点,则Rt△ABC的面积为_________。
经过C点,则Rt△ABC的面积为_________。
【答案】![]()
【解析】试题解析:过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,

∵A点的横坐标是2,且在双曲线y═![]() (m>0)上,
(m>0)上,
∴A(2,2m),
∵∠ABC=90°,
∴∠ABE+∠CBF=∠FCB+∠CBF=90°,
∴∠ABC=∠FCB,
∴△ABE∽△BCF,
∴![]() ,
,
∴CF=1,BF=![]() ,
,
∴C(-1-![]() ,1),
,1),
∵双曲线y=-![]() 经过C点,
经过C点,
∴-1-![]() =-m,
=-m,
∴m=3,
∴A(2,6),C(-3,1),
∴AE=6,CF=1,EF=5,BF=3-1=2,BE=1+2=3,
∴Rt△ABC的面积=S梯形ACFE-S△BCF-S△ABE=![]() (6+1)×5-
(6+1)×5-![]() ×2×1-
×2×1-![]() ×3×6=
×3×6=![]() .
.

练习册系列答案
相关题目