题目内容
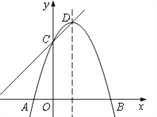
【题目】已知抛物线y＝ax 2＋bx＋c经过A（－1，0）、B（3，0）、C（0，3）三点，顶点为D，点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，则点P的坐标为_______________。
【答案】
【解析】试题解析：抛物线y＝ax 2＋bx＋c经过A（－1，0）、B（3，0）、C（0，3）三点
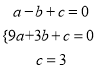，解得
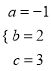
∴y=
∴抛物线的对称轴为直线x=1，D点坐标为（1，4），
设P（1，a），过点P作PH⊥DM于H，连接PA、PB，如图，
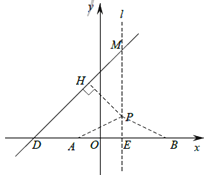
则MP=4-a，又∠HMP=45°，
∴HP=AP=
，
Rt△APE中，AP2=AE2+PE2，即：(
)2＝a2+4，
解得： 
∴P1（1，-4+2
），P2（1，-4-2
）
练习册系列答案
相关题目
