Question

【题目】如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是（ ）

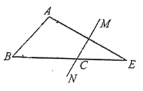
A. 45°B. 60°C. 50°D. 25°

Answer 1

【答案】C

【解析】

首先连接AC，由AE的垂直平分线MN交BE于点C，可得AC=EC，又由AB+BC=BE，易证得AB=AC，然后由等腰三角形的性质与三角形内角和定理，求得∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°，继而求得答案．

连接AC，

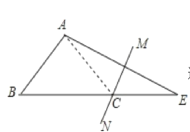
∵MN是AE的垂直平分线，

∴AC=EC，

∴∠CAE=∠E，

∵AB+BC=BE，BC+EC=BE，

∴AB=EC=AC，

∴∠B=∠ACB，

∵∠ACB=∠CAE+∠E=2∠E，

∴∠B=2∠E，

∴∠BAC=180°∠B∠ACB=180°4∠E，

∵∠BAE=∠BAC+∠CAE=180°4∠E+∠E=105°

解得：∠E=25°，

∴∠B=2∠E=50°.

故选：C.