Question

【题目】如图，长方形ABCD被分成六个小的正方，已知中间一个小正方形的边长为1，其它正方形的边长分别为a、b、c、d．观察图形并探索：（1）b＝_____，d＝_____；（用含a的代数式表示）（2）长方形ABCD的面积为_____．

Answer 1

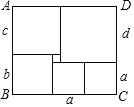
【答案】a+1 2a﹣1 143

【解析】

（1）利用中间一个小正方形的边长为1，得出b，d与a的关系；

（2）利用c＝b+1，b＝a+1，得出c＝a+2，再利用c＝d﹣1，d＝2a﹣1，得出c＝2a﹣2，那么2a﹣2＝a+2，解方程求出a的值，然后分别计算出长方形ABCD的长与宽，进而求出面积．

（1）∵中间一个小正方形的边长为1，

∴b＝a+1，d＝2a﹣1；

故答案为：a+1，2a﹣1；

（2）∵c＝b+1，b＝a+1，

∴c＝a+2，

又∵c＝d﹣1，d＝2a﹣1，

∴c＝2a﹣2，

∴2a﹣2＝a+2，

解得a＝4．

则长方形ABCD的长为c+d＝a+2+2a﹣1＝3a+1＝13，

宽为a+d＝a+2a﹣1＝3a﹣1＝11，

所以长方形ABCD的面积为：11×13＝143．

故答案为：143．