题目内容
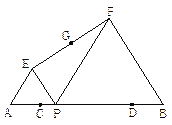
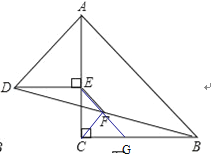
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=![]() EF;
EF;
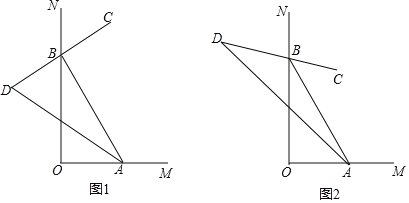
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

【答案】(1)EF =2.5;(2)证明见解析;(3)(1)中的结论仍然成立.理由见解析.
【解析】试题分析:(1)等腰直角三角形的斜边长是直角边的![]() 倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
(2)连接CF,需要证明![]() 是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得
是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得![]() 从而
从而![]() ,再根据直角三角形斜边上的中线是斜边的一半,得
,再根据直角三角形斜边上的中线是斜边的一半,得![]() ,得证
,得证![]() 是等腰直角三角形,结论得证;
是等腰直角三角形,结论得证;
(3)连接CF,延长EF交CB于点G,利用ASA证明△EDF≌△GBF,得出EF=GF,BG=DE=AE,进而证明CE=CG,得出△CEF为等腰直角三角形,利用三线合一证明![]() 结论得证。
结论得证。
试题解析:
(1)∵∠AED=90°,AE=DE,AD=3![]() ,
,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF=![]() BD=2.5;
BD=2.5;
(2)连接CF,线段CE与FE之间的数量关系是CE=![]() FE;
FE;
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=![]() EF.
EF.
(3)(1)中的结论仍然成立.
如图,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
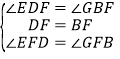 ,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=![]() FE;
FE;

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.