题目内容
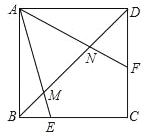
【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
【答案】（1）b=﹣2a，顶点D的坐标为（﹣
，﹣
）；（2）
；（3） 2≤t＜
．
【解析】试题分析：（1）把M点坐标代入抛物线解析式可得到b与a的关系，可用a表示出抛物线解析式，化为顶点式可求得其顶点D的坐标；
（2）把点
代入直线解析式可先求得m的值，联立直线与抛物线解析式，消去y，可得到关于x的一元二次方程，可求得另一交点N的坐标，根据a<b，判断a<0，确定D、M、N的位置，画图1，根据面积和可得
的面积即可；
（3）先根据a的值确定抛物线的解析式，画出图2，先联立方程组可求得当GH与抛物线只有一个公共点时，t的值，再确定当线段一个端点在抛物线上时，t的值，可得：线段GH与抛物线有两个不同的公共点时t的取值范围．
试题解析：(1)∵抛物线
有一个公共点M(1,0)，
∴a+a+b=0，即b=2a，
∴抛物线顶点D的坐标为
(2)∵直线y=2x+m经过点M(1,0)，
∴0=2×1+m，解得m=2，
∴y=2x2，
则
得
∴(x1)(ax+2a2)=0,
解得x=1或
∴N点坐标为
∵a<b，即a<2a，
∴a<0，
如图1，设抛物线对称轴交直线于点E，
∵抛物线对称轴为
设△DMN的面积为S，
(3)当a=1时，
抛物线的解析式为：
有
解得：
∴G(1,2)，
∵点G、H关于原点对称，
∴H(1,2)，
设直线GH平移后的解析式为：y=2x+t，
x2x+2=2x+t，
x2x2+t=0，
△=14(t2)=0，
当点H平移后落在抛物线上时,坐标为(1,0)，
把(1,0)代入y=2x+t，
t=2，
∴当线段GH与抛物线有两个不同的公共点,t的取值范围是
【题型】解答题
【结束】
24
【题目】在△ABC中，AB=AC，点D是直线BC上的一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE，设∠BAC=α，∠BCE=β．
（1）如图①，当点D在线段BC上，如果α=60°，β=120°；
如图②，当点D在线段BC上，如果α=90°，β=90°
如图③，当点D在线段BC上，如果α，β之间有什么样的关系？请直接写出．
（2）如图④，当点D在射线BC上，（1）中结论是否成立？请说明理由．
（3）如图⑤，当点D在射线CB上，且在线段BC外，（1）中结论是否成立？若不成立，请直接写出你认为正确的结论．
【答案】（1）α+β=180°；（2）（1）中结论是成立；（3）（1）中结论是不成立，成立的是：∠BAC+∠CBE=180°．
【解析】试题分析：（1）先判断出△ABD≌△ACE得出∠ABD=∠ACE，再用三角形的内角和即可得出结论；
（2）同（1）的方法即可得出结论；
（3）先判断出△ABE≌△ACD，再用三角形的内角和即可得出结论．
试题解析：解：（1）α+β=180°．理由如下：
如图③．∵∠BAC=∠DAE，∴∠BAD=∠CAE．在△ABD和△ACE中，
，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE．在△ABC中，∠BAC+∠B+∠ACB=180°，∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°，即：α+β=180°；
（2）（1）中结论是成立，理由如下：
如图④，连接CE．∵∠BAC=∠DAE，∴∠BAD=∠CAE．在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE．在△ABC中，∠BAC+∠B+∠ACB=180°，∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°，即：α+β=180°；
（3）（1）中结论是不成立，成立的是：∠BAC+∠CBE=180°．理由如下：
如图⑤，连接BE．∵∠BAC=∠DAE，∴∠BAE=∠CAD．在△ABE和△ACE中，
，∴△ABE≌△ACD（SAS），∴∠ABE=∠ACD．在△ABC中，∠BAC+∠ABC+∠ACD=180°，∴∠BAC+∠ABC+∠ABE=∠BAC+∠CBE=180°，即：∠BAC+∠CBE=180°．
