Question

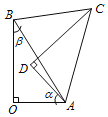
【题目】如图，△AOB≌△ADC，点B和点C是对应顶点，∠O＝∠D＝90°，记∠OAD＝α，∠ABO＝β，当BC∥OA时，α与β之间的数量关系为（　　）

A.α＝βB.α＝2βC.α+β＝90°D.α+β＝180°

Answer 1

【答案】B

【解析】

根据全等三角形对应边相等可得AB＝AC，由全等三角形对应角相等可得∠BAO＝∠CAD，然后求出∠BAC＝α，再根据等腰三角形两底角相等求出∠ABC，然后根据两直线平行，同旁内角互补表示出∠OBC，整理即可．

解：∵△AOB≌△ADC，

∴AB＝AC，∠BAO＝∠CAD，

∴∠BAC＝∠OAD＝α，

在△ABC中，∠ABC＝（180°﹣α），

∵BC∥OA，

∴∠OBC＝180°﹣∠O＝180°﹣90°＝90°，

∴∠OBC=β+（180°﹣α）＝90°，

整理得，α＝2β．

故选：B．