题目内容
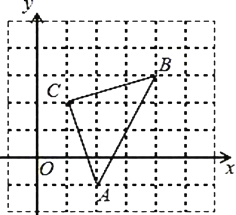
【题目】如图,点![]() 的坐标为
的坐标为![]() ,作
,作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 、
、![]() 上沿
上沿![]() 运动,当
运动,当![]() 时,点
时,点![]() 的坐标为________.
的坐标为________.

【答案】(2,4)或(4,2)
【解析】
根据点B的坐标和已知条件可得AO=OC=AB=BC=4,∠OAB =∠COD =∠OCB=90°,OD=2,然后根据点P的位置分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可求出结论.
解:∵点![]() 的坐标为
的坐标为![]() ,
,![]() 轴,
轴,![]() 轴,点
轴,点![]() 为线段
为线段![]() 的中点,
的中点,
∴AO=OC=AB=BC=4,∠OAB =∠COD =∠OCB=90°,OD=2
①当点P在AB上时,如下图所示

在Rt△OAP和Rt△COD中
![]()
∴Rt△OAP≌Rt△COD
∴AP=OD=2
∴点P的坐标为(4,2);
②当点P在BC上时,如下图所示

在Rt△OCP和Rt△COD中
![]()
∴Rt△OCP≌Rt△COD
∴CP=OD=2
∴点P的坐标为(2,4);
综上:点P的坐标为(2,4)或(4,2)
故答案为:(2,4)或(4,2).

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.