题目内容
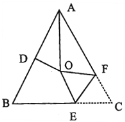
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )
A.120°B.108°C.110°D.102°
【答案】B
【解析】
连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形的内角和定理列式计算即可得解.
解:如图,连接OB、OC,

∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
又∵AB=AC,
∴∠ABC=![]() (180°
(180°![]() ∠BAC)=
∠BAC)=![]() (180°
(180°![]() 54°)=63°,
54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°![]() 27°=36°,
27°=36°,
∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°![]() ∠COE
∠COE![]() ∠OCB=180°
∠OCB=180°![]() 36°
36°![]() 36°=108°;
36°=108°;
故选:B.

练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目