题目内容
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() .
.
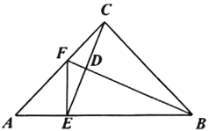
(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)70°;30°;(2)见解析
【解析】
(1)根据等边对等角求出∠CAB和∠CBA的度数,再根据等边对等角求出∠BEC和∠BCE的度数,从而可得出∠ACE的度数,最后根据外角的性质可求出∠BEC的度数;再证明△BCF≌△BEF,从而得出∠BEF的度数,最后得出∠FEC的度数.
(2)先根据(1)中全等得出EF=CF,再由等角对等边判定△AEF为等腰三角形,得出AE=EF,从而得出结果.
证明:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,∴∠CBF=∠EBF,
,∴∠CBF=∠EBF,
在△BCF和△BEF中,
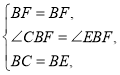
∴△BCF≌△BEF(SAS).
∴∠BEF=∠BCF=100°,.
∴∠FEC=∠BEF-∠BEC=30°.
(2)由(1)可知![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
(1)在表中的频数分布表中,m= ,n= .
成绩 | 频数 | 频率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)请补全图中的频数分布直方图.

(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?