题目内容
【题目】如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.
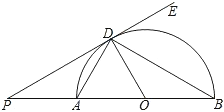
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BDE=60°,PD=![]() ,求PA的长.
,求PA的长.
【答案】(1)PD是⊙O的切线.(2)1.
【解析】
试题分析:(1)要证是直线PD是为⊙O的切线,需证∠PDO=90°.因为AB为直径,所以∠ADO+∠ODB=90°,由∠PDA=∠PBD=∠ODB可得∠ODA+∠PDA=90°,即∠PDO=90°.
(2)根据已知可证△AOD为等边三角形,∠P=30°.在Rt△POD中运用三角函数可求解.
解:(1)PD是⊙O的切线.理由如下:
∵AB为直径,
∵∠ADB=90°,
∴∠ADO+∠ODB=90°.
∵∠PDA=∠PBD=∠ODB,
∴∠ODA+∠PDA=90°.即∠PDO=90°.
∴PD是⊙O的切线.
(2)∵∠BDE=60°,∠ADB=90°,
∴∠PDA=180°﹣90°﹣60°=30°,
又PD为半圆的切线,所以∠PDO=90°,
∴∠ADO=60°,又OA=OD,
∴△ADO为等边三角形,∠AOD=60°.
在Rt△POD中,PD=![]() ,
,
∴OD=1,OP=2,
PA=PO﹣OA=2﹣1=1.


练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目