题目内容
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
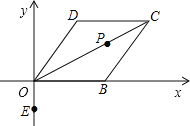
(1)点D的坐标为 ,点C的坐标为 ;
(2)若点P是对角线OC上一动点,点E(0,﹣![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
【答案】(1)(1,![]() ),(3,
),(3,![]() );
);
(2)![]() .
.
【解析】
试题分析:(1)作DF⊥OB于点F,在直角△ODF中利用三角函数求得DF和OF的长,则D的坐标即可求得,然后根据CD∥OB,则C的坐标即可求得;
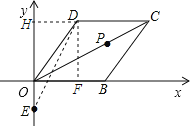
(2)B关于OC的对称点是D,则DE的长就是PE+PB的最小值,作DH⊥y轴于点H,首先在直角△OGH中利用勾股定理求得DH和OH的长,然后在直角△HED中利用勾股定理求解.
解:(1)作DF⊥OB于点F.
∵B的坐标是(2,0),
∴OB=2,
∴菱形OBCD中,OD=OB=CD=2,
在直角△ODF中,DF=ODsin∠DOB=2×![]() =
=![]() ,OF=ODcos∠DOB=2×
,OF=ODcos∠DOB=2×![]() =1,
=1,
则D的坐标是(1,![]() ).
).
则C的坐标是(3,![]() ).
).
故答案是:(1,![]() ),(3,
),(3,![]() );
);
(2)作DH⊥x轴于点H,连接DE.
在直角△OGH中,∠HOG=90°﹣∠DOB=90°﹣60°=30°.
GH=ODsin∠HOG=2×![]() =1,OH=OGcos∠HOG=2×
=1,OH=OGcos∠HOG=2×![]() =
=![]() .
.
则HE=2![]() .
.
在直角△HEG中,DE=![]() =
=![]() =
=![]() .
.
即PE+PB的最小值是![]() .
.

练习册系列答案
相关题目