Question

【题目】如图，二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于点C，且B（1，0），C（0，3），将△BOC绕点O按逆时针方向旋转90°，C点恰好与A重合．

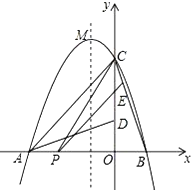
（1）求该二次函数的解析式；

（2）若点P为线段AB上的任一动点，过点P作PE∥AC，交BC于点E，连结CP，求△PCE面积S的最大值；

（3）设抛物线的顶点为M，Q为它的图象上的任一动点，若△OMQ为以OM为底的等腰三角形，求Q点的坐标．

Answer 1

【答案】（1）y=﹣x2﹣2x+3（2）（3）Q（，），或（，）

【解析】试题分析：（1）根据题意求出A、B、C的坐标，然后根据待定系数法求函数的解析式即可；

（2）设点P（x，0），则PB=1﹣x，根据三角形的面积可得二次函数的解析式，然后根据二次函数的最值可求解；

（3）根据配方法求出顶点的坐标，然后根据等腰三角形的性质，结合勾股定理列方程可求解.

试题解析：（1）∵B（1，0），C（0，3），∴OB=1，OC=3．

∵△BOC绕点O按逆时针方向旋转90°，C点恰好与A重合．

∴OA=OC=3，∴A（﹣3，0），

∵点A，B，C在抛物线上，

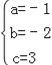∴，∴，∴二次函数的解析式为y=﹣x2﹣2x+3，

（2）设点P（x，0），则PB=1﹣x，

∴S△PBE=（1﹣x）2，

∴S△PCE=S△PBC﹣S△PBE=PB×OC﹣（1﹣x）2=（1﹣x）×3﹣（1﹣x）2=﹣（x﹣1）2+，

当x=1时，S△PCE的最大值为．

（3）∵二次函数的解析式为y=﹣x2﹣2x+3=﹣（x+1）2+4，

∴顶点坐标（﹣1，4），

∵△OMQ为等腰三角形，OM为底，

∴MQ=OQ，

∴=，

∴8x2+18x=7=0，∴x=，∴y=或y=，

∴Q（，），或（，）．