题目内容
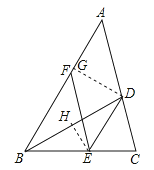
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=12,求DE的长及四边形ADEF的面积.
【答案】(1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形,
∠ABD=∠BDE,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)解:如图,过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠ABD=∠EBD=30°,
∴DG=![]() BD=
BD=![]() ×12=6,
×12=6,
∵BE=DE,
∴BH=DH=![]() BD=6,
BD=6,
∴BE=![]() =
=![]() .
.
∴DE=BE=![]() ,
,
∴四边形ADEF的面积为:DEDG=![]() .
.
【解析】(1)由DE∥AB,EF∥AC,可证得四边形ADEF是平行四边形,∠ABD=∠BDE,又由BD是△ABC的角平分线,易得△BDE是等腰三角形,即可证得结论;
(2)首先过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,易求得DG与DE的长,继而求得答案.

练习册系列答案
相关题目
【题目】从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86分,方差如下表,你认为派谁去参赛更合适( )
选手 | 甲 | 乙 | 丙 | 丁 |
方差 | 1.5 | 2.6 | 3.5 | 3.68 |
A.甲B.乙C.丙D.丁