题目内容
【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
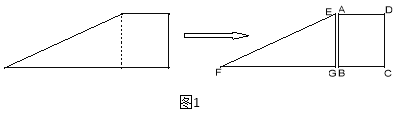
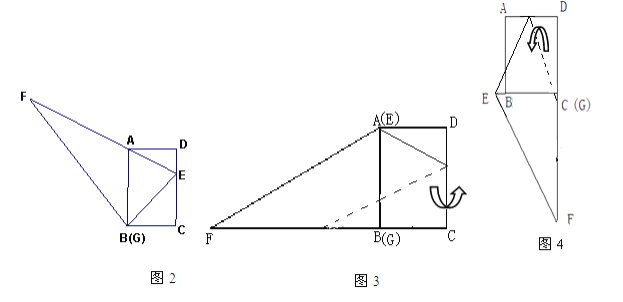
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
【答案】(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等.
【解析】
试题分析:(1)利用矩形的性质以及得出△ADE∽△FBE,求出即可;
(2)根据Rt△F,HN~Rt△F,EG,得到HN=3,从而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,从而S△B,C,G=144,进行比较即可.
⑴BE=AD=15,在RtBCE中,CE2=B E2-BC2=152-122,求得CE=9,DE=6,
证Rt△ADE~Rt△FBE,
求得BF=30
⑵①如图1,将矩形ABCD和Rt△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,

由Rt△F,HN~Rt△F,EG,得到HN=3,
从而S△AMH=144
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,

从而S△B,C,G=144,∴未包裹的面积为144.
∴按照二种包裹的方法未包裹的面积相等。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目