题目内容
【题目】如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(4,0),经过点A点B抛物线y=x+bx+c与y轴交于点C.
(1)求抛物线的关系式.
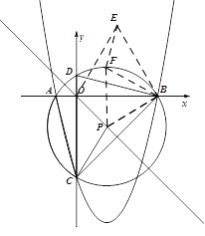
(2)△ABC的外接圆与y轴交于点D,在抛物线上是否存在点M使S△MBC=S△DBC,若存在,请求出点M的坐标.
(3)点P是直线y=-x上一个动点,连接PB,PC,当PB+PC+PO最小时,求点P的坐标及其最小值.

【答案】(1)抛物线关系式:y=x-3x-4;(2)点M(5,6)(3)P(2-![]() ,
, ![]() -2)
-2)
【解析】试题分析:(1)用代入法直接求函数解析式;(2)存在,连接AD,过点D做直线l∥BC,则求出直线l的关系式为:y=x+1,再求它与![]() 的交点坐标,即可;(3)把△BPO绕点B顺时针旋转60°得△BFE,连接FP得等边△BFP, 则PB+PC+PO=PC+PF+FE,所以连接EC与直线y=-x交于点P,则点P即为所求. 先求出直线EC关系式为:y=(
的交点坐标,即可;(3)把△BPO绕点B顺时针旋转60°得△BFE,连接FP得等边△BFP, 则PB+PC+PO=PC+PF+FE,所以连接EC与直线y=-x交于点P,则点P即为所求. 先求出直线EC关系式为:y=(![]() +2)x-4,再联立y=-x得出P的坐标即可;
+2)x-4,再联立y=-x得出P的坐标即可;
试题解析:
(1)把点A(-1,0),点B(4,0)代入y=x+bx+c得:
![]()
解得: ![]()
∴0抛物线关系式:y=x-3x-4
(2)连接AD,
把x=0代入y=x+bx+c得y=-4.
∴OC=OB=4.
∴∠ABC=45°.
∴∠ADC=45°
∵OA=1,
∴OD=1
过点D做直线l∥BC,则直线l的关系式为:y=x+1
联立抛物线关系式得:
![]()
解得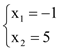
∴点M(5,6)
(3)把△BPO绕点B顺时针旋转60°得△BFE,
连接FP得等边△BFP,
∴PB+PC+PO=PC+PF+FE
∴连接EC与直线y=-x交于点P,则点P即为所求.
在等边△OBE中
∵OB=4
∴点E(2, ![]() )
)
又∵点C(0,-4)
∴直线EC关系式为:y=(![]() +2)x-4
+2)x-4
联立y=-x得
点P(2-![]() ,
, ![]() -2)
-2)