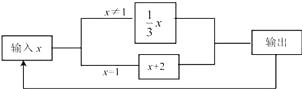
��Ŀ����
����Ŀ��ʵ����̽����������������1��3��5��7�����г���ͼ��������ʮ�ֿ���5��������ͼ�� 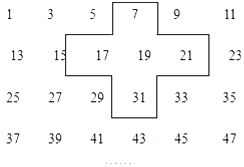
��1������ʮ�ֿ���������ƽ�ƣ���һ��Ҫ��ס�����е�5�����������м����Ϊa����a�Ĵ���ʽ��ʾʮ�ֿ��ס��5������֮�ͣ�
��2��ʮ�ֿ��ס��5����֮���ܵ���2015�����ܣ��ֱ�д��ʮ�ֿ��ס��5�����������ܣ���˵�����ɣ�
��3��ʮ�ֿ��ס��5����֮���ܵ���365�����ܣ��ֱ�д��ʮ�ֿ��ס��5�����������ܣ���˵�����ɣ�
���𰸡�
��1���⣺�ӱ���֪���м����Ϊa�������Ϊa��12�������Ϊa+12�������Ϊa��2�������Ϊa+2��
a+��a��2��+��a+2��+��a��12��+��a+12��=5a
��2���⣺5a=2015��
a=403��
��403��������
������ǿ��Ե�
��3���⣺5a=365��
a=73��
��73λ��һ�е�����ߣ�
��ʮ�ֿ��ס��5����֮�Ͳ��ܵ���365
����������1���۲�ʮ�ֿ��ס�����ݵ����й��ɵõ������ĸ���Ϊa��12��a��2��a+2��a+12��Ȼ�����úϲ�ͬ������5�����ĺͣ���2���ⷽ��5a=2015��a=403������ʮ�ֿ���ڵ�����������������ʮ�ֿ��ס��5����֮���ܵ���2015����3���ⷽ��5a=365�����a=73��Ȼ��ȷ��73����λ�ü��ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�