Question

【题目】如图所示：已知中，，在内部作分别交于点

[操作]（1）将绕点逆时针旋转，使边与边重合，把旋转后点的对应点记作点，得到，请在图中画出;(不写出画法)

[探究]（2）在作图的基础上，连接， 求证：

[拓展]（3）写出线段和之间满足的数量关系，并简要说明理由．

Answer 1

【答案】（1）见详解；（2）见详解；（3）MN2=BM2+NC2，理由见详解.

【解析】

（1）根据旋转中心、旋转方向和旋转角度进行作图即可；

（2）先根据SAS判定△MAN≌△QAN，进而得出结论；

（3）再由全等三角形和旋转的性质，得出MN=NQ，MB=CQ，最后根据Rt△NCQ中的勾股定理得出结论；

解：（1）如图，△ACQ即为所求；

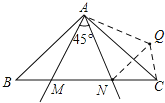
（2）证明：由旋转可得，△ABM≌△ACQ，

∴AM=AQ，∠BAM=∠CAQ
∵∠MAN=45°，∠BAC=90°

∴∠BAM+∠NAC=45°
∴∠CAQ+∠NAC=45°，即∠NAQ=45°
在△MAN和△QAN中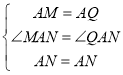
，

∴△MAN≌△QAN（SAS），
∴MN=NQ；
（3）MN2=BM2+NC2；

由（2）中可知，MN=NQ，MB=CQ，

又∠NCQ=∠NCA+ACQ=∠NCA+∠ABM=45°+45°=90°

在Rt△NCQ中，有

NQ2=CQ2+NC2，

即MN2=BM2+NC2；