题目内容
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
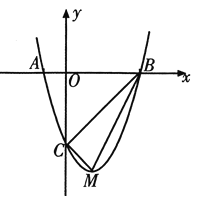
【答案】(1)![]() ;(2)△BCM是Rt△;(3)O(0,0),P1(0,
;(2)△BCM是Rt△;(3)O(0,0),P1(0, ![]() ),P2(9,0).
),P2(9,0).
【解析】试题分析:(1)已知抛物线图象上的三点坐标,可用待定系数法求出该抛物线的解析式;
(2)根据B、C、M的坐标,可求得△BCM三边的长,然后判断这三条边的长是否符合勾股定理即可;
(3)假设存在符合条件的P点;首先连接AC,根据A、C的坐标及(2)题所得△BDC三边的比例关系,即可判断出点O符合P点的要求,因此以P、A、C为顶点的三角形也必与△COA相似,那么分别过A、C作线段AC的垂线,这两条垂线与坐标轴的交点也符合点P点要求,可根据相似三角形的性质(或射影定理)求得OP的长,也就得到了点P的坐标.
解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3![]() ,BM=2
,BM=2![]() ,CM=
,CM=![]() ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)若∠APC=90°,即P点和O点重合,如图1,

连接AC,
∵∠AOC=∠MCB=90°,且![]() =
=![]() ,
,
∴Rt△AOC∽Rt△MCB,
∴此时P点坐标为(0,0).
若P点在y轴上,则∠PAC=90°,如图2,过A作AP1⊥AC交y轴正半轴于P1,
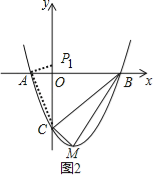
∵Rt△CAP1∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴点P1(0,![]() ).
).
若P点在x轴上,则∠PCA=90°,如图3,过C作CP2⊥AC交x轴正半轴于P2,
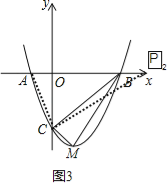
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,![]() ),P2(9,0).
),P2(9,0).