题目内容
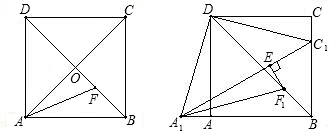
如图，E为正方形ABCD内的一点，△ABE为正三角形，求∠CED的度数．
∵四边形ABCD是正方形，
∴∠BAD=∠ADC=90°，AB=AD=BC．
∵△ABE为正三角形，
∴∠BAE=60°，AE=AB=BE，
∴AE=BE=AD=BC，
∴∠DAE=∠BAD-∠BAE=90°-60°=30°．
∵AD=AE，∴∠ADE=（180°-30°）÷2=75°．
∴∠EDC=90°-75°=15°．
同理可得∠ECD=15°．
∴∠CED=180°-2×15°=150°．
∴∠BAD=∠ADC=90°，AB=AD=BC．
∵△ABE为正三角形，
∴∠BAE=60°，
AE=AB=BE，∴AE=BE=AD=BC，
∴∠DAE=∠BAD-∠BAE=90°-60°=30°．
∵AD=AE，∴∠ADE=（180°-30°）÷2=75°．
∴∠EDC=90°-75°=15°．
同理可得∠ECD=15°．
∴∠CED=180°-2×15°=150°．
练习册系列答案
一本好题口算题卡系列答案
相关题目
