题目内容
【题目】如图,将图一中的等腰直角三角形纸片ABC,依次沿着折痕DE,FG翻折,得到图二中的五边形ADEGF.若图二中,DF∥EG,点C′,B′恰好都是线段DF的三等分点,GC′交EB′于点O,EG=4![]() ﹣2,则等腰直角三角形ABC的斜边BC的长为( )
﹣2,则等腰直角三角形ABC的斜边BC的长为( )
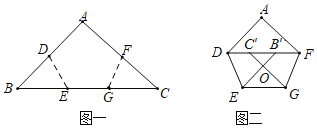
A.4![]() +6B.4
+6B.4![]() ﹣6C.8
﹣6C.8![]() +4D.8﹣4
+4D.8﹣4![]()
【答案】A
【解析】
由题意根据折叠得FC=FC′,DB=DB′,∠C=∠FC′G=45°,进而得出四边形CFC′G是菱形,设DC′=x,表示其它的边长,在等腰直角三角形中,利用边角关系,表示边长,然后在等腰直角三角形ABC中,依据边角关系,距离方程求出未知数,进而求出斜边BC的长.
解:由折叠得:FC=FC′,DB=DB′,∠C=∠FC′G=45°,
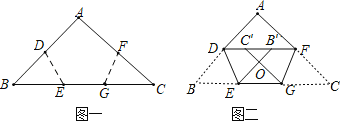
∵DF∥BC,
∴∠FC′G=∠C′GE=∠C=45°,
∴C′G∥AC,
∴四边形CFC′G是菱形,
∴CF=FC′=C′G=GC,
同理:BE=BD=DB′=EB′,
设DC′=x,则DF=3x,BE=CG=2x,
在等腰直角三角形ADF中,AF=AD=![]() DF=
DF=![]() ,
,
∴AC=AF+FC=![]() +2x=
+2x=![]() ,
,
在在等腰直角三角形ABC中,AB=AC=![]() BC,
BC,
∴![]() =
=![]() (4x+4
(4x+4![]() ﹣2),
﹣2),
解得:x=2,
∴BC=4x+4![]() ﹣2=4
﹣2=4![]() +6.
+6.
故选:A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
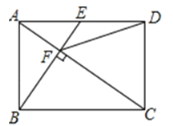
小学生10分钟应用题系列答案【题目】在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,对于结论①CF=2AF②△AEF∽△CAB③DF=DC④tan∠CAD=![]() 正确的有_______________.
正确的有_______________.
【题目】为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过![]() 吨,那么这个月该单元居民只交10元水费.如果超过
吨,那么这个月该单元居民只交10元水费.如果超过![]() 吨,则这个月除了仍要交10元水费外,超过那部分按每吨
吨,则这个月除了仍要交10元水费外,超过那部分按每吨![]() 元交费.
元交费.
(1)该单元居民8月份用水80吨,超过了“规定的![]() 吨”,则超过部分应交水费 (80-x)
吨”,则超过部分应交水费 (80-x)
元(用含x的式子表示).
(2)下表是该单元居民9月、10月的用水情况和交费情况:
月份 | 用水量(吨) | 交费总数(元) |
9月份 | 85 | 25 |
10月份 | 50 | 10 |
根据上表数据,求该x吨是多少?