题目内容
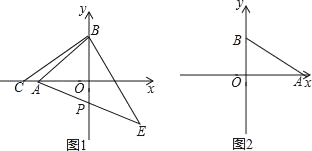
【题目】已知:如图1,△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. 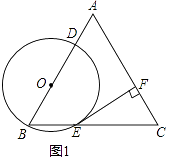
(1)求证:直线EF是⊙O的切线;
(2)如图2,当直线AC与⊙O相切时,求⊙O的半径. 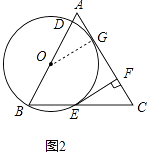
【答案】
(1)证明:连接OE.

∵△ABC是等边三角形∴∠B=∠C=60°;
又∵OB=OE∴∠OEB=∠B=∠C=60°;
∴OE∥AC;
∵EF⊥AC,
∴EF⊥OE
∴EF是⊙O的切线.
(2)设直线AC与⊙O相切于点G,连接OG,则OB=OG=r,OA=4﹣r
在Rt△AOG中,sinA= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:r=8 ![]() ﹣12.
﹣12.
【解析】(1)连接OE,只要证明OE⊥EF,只要证明OE∥AC即可解决问题.(2)设直线AC与⊙O相切于点G,连接OG,则OB=OG=r,OA=4﹣r,在Rt△AOG中,根据sinA= ![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目
【题目】某超市购进一批文具袋,每个进价为10元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元 | 11 | 12 | 13 | 14 | 15 | … |
销售数量y(个) | 38 | 36 | 34 | 32 | 30 | … |
备注:物价局规定,每个文具袋的售价不低于10元且不高于18元 | ||||||
请你根据表中信息解答下列问题:
(1)y是x的函数,其函数关系式为
(2)营业员发现有一天的利润是150元,则销售单价为元.
(3)试销售的目的是想要每天获得最大的销售利润.请你帮助销售经理计算一下,在这种情况下单价x(元)应定为多少时,每天的销售利润w(元)最大,最大利润是多少元?