题目内容
【题目】某超市购进一批文具袋,每个进价为10元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元 | 11 | 12 | 13 | 14 | 15 | … |
销售数量y(个) | 38 | 36 | 34 | 32 | 30 | … |
备注:物价局规定,每个文具袋的售价不低于10元且不高于18元 | ||||||
请你根据表中信息解答下列问题:
(1)y是x的函数,其函数关系式为
(2)营业员发现有一天的利润是150元,则销售单价为元.
(3)试销售的目的是想要每天获得最大的销售利润.请你帮助销售经理计算一下,在这种情况下单价x(元)应定为多少时,每天的销售利润w(元)最大,最大利润是多少元?
【答案】
(1)一次;y=﹣2x+60
(2)15
(3)解:由题意得w=(﹣2x+60)(x﹣10)=﹣2x2+80x﹣600=﹣2(x﹣20)2+200,
∵a=﹣2<0,
∴当x<20时,w随x的增大而增大,
∵10≤x≤18,
∴当x=18时,w最大,最大值为﹣2(18﹣20)2+200=192,
答:文具袋的单价应定为18元时,每天的销售利润w最大,最大利润是192元.
【解析】解:(1.)由表格可知,销售单价每增加1元,其销售数量就减少2件, ∴y是x的一次函数,
设y=kx+b,
将x=11、y=38,x=12、y=36代入,得:![]() ,
,
解得: ![]() ,
,
∴y=﹣2x+60,
所以答案是:一次,y=﹣2x+60;
(2.)根据题意,得:(x﹣10)(﹣2x+60)=150,
整理,得:x2﹣40x+375=0,
解得:x=15或x=25,
∵每个文具袋的售价不低于10元且不高于18元,
∴销售单价x=15,
所以答案是:15;

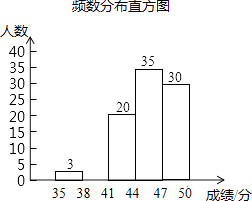
【题目】为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率 |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)样本的中位数是分;
(2)频率统计表中a= , b=;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?