ЬтФПФкШн
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌAЃЈaЃЌ0ЃЉЁЂBЃЈbЃЌ0ЃЉЧвaЁЂbТњзу|a+4|+![]() =0
=0
ЂйЧѓaЁЂbЕФжЕЃЛ
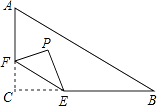
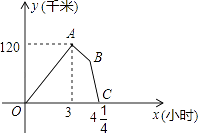
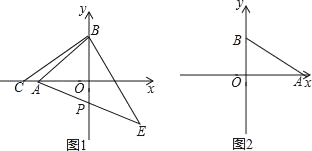
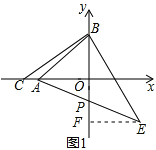
ЂкШєCЃЈЉ6ЃЌ0ЃЉЃЌСЌCBЃЌзїBEЁЭCBЃЌДЙзуЮЊBЃЌЧвBC=BEЃЌСЌAEНЛyжсгкPЃЌЧѓPЕузјБъЃЛ
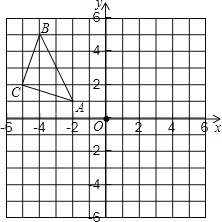
ЃЈ2ЃЉШчЭМ2ЃЌШєAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌЕуQДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЩшЕуQдЫЖЏЪБМфЮЊtУыЃЌЙ§QЕузїжБЯпABЕФДЙЯпЃЌДЙзуЮЊDЃЌжБЯпQDгыyжсНЛгкEЕуЃЌдкЕуQЕФдЫЖЏЙ§ГЬжаЃЌвЛЖЈДцдкЁїEOQЁеЁїAOBЃЌЧыжБНгаДГіДцдкЕФtжЕвдМАЯргІЕФEЕузјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйa=-4ЃЌb=4ЃЛЂкЙ§EЕузїyжсДЙЯпМДПЩЃЌPЃЈ0ЃЌ-2ЃЉЃЛЃЈ2ЃЉСНжжЧщПіЃКЕБt=3ЪБЃЌЕуEЮЊЃЈ0ЃЌ-6ЃЉЃЛЕБt=9ЪБЃЌЕуEЮЊЃЈ0ЃЌ6ЃЉЃЎ
ЁОНтЮіЁП
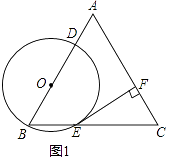
ЪдЬтЃЈ1ЃЉБОЬтПМВщШ§НЧаЮШЋЕШЕФХаЖЈЃЌИљОнЬтФПжаЕФаХЯЂЧѓГіЯргІЕФЕуЕФзјБъЃЌПЩвдИљОнЬтФПжаЕФаХЯЂЛГіЯргІЕФЭМаЮЃЌЙиМќЪЧе§ШЗЗжЮіЬтФПжаЕФаХЯЂЃЌЧѓГіЫљвЊЧѓЕФНсТлЃЎЂйгЩaЁЂbТњзу![]() ЃЌПЩвдЧѓЕУaЁЂbЕФжЕЃЎЂкзїEFЁЭyжсгкЕуFЃЌИљОнЬтФПжаЕФаХЯЂЃЌПЩвдЭЦГіЁїBCOЁеЁїEBFЃЌШЛКѓИљОнЖдгІЙиЯЕЧѓГіЖдгІБпЕФГЄЖШЃЌДгЖјПЩвдЧѓЕУЕуPЕФзјБъЃЎЃЈ2ЃЉИљОнЬтвтПЩвдЛГіЯргІЕФЭМЯѓЃЌДгЖјПЩвджБНгаДГіtЕФжЕКЭЯргІЕФЕуEЕФжЕЃЎ
ЃЌПЩвдЧѓЕУaЁЂbЕФжЕЃЎЂкзїEFЁЭyжсгкЕуFЃЌИљОнЬтФПжаЕФаХЯЂЃЌПЩвдЭЦГіЁїBCOЁеЁїEBFЃЌШЛКѓИљОнЖдгІЙиЯЕЧѓГіЖдгІБпЕФГЄЖШЃЌДгЖјПЩвдЧѓЕУЕуPЕФзјБъЃЎЃЈ2ЃЉИљОнЬтвтПЩвдЛГіЯргІЕФЭМЯѓЃЌДгЖјПЩвджБНгаДГіtЕФжЕКЭЯргІЕФЕуEЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйЁпaЁЂbТњзу|a+4|+![]() =0ЃЌ Ёрa+4=0ЃЌa+b=0ЃЎ НтЕУЃЌa=-4ЃЌb=4ЃЎ
=0ЃЌ Ёрa+4=0ЃЌa+b=0ЃЎ НтЕУЃЌa=-4ЃЌb=4ЃЎ
ЂкШчЭМЫљЪОЃКзїEFЁЭyжсгкЕуFЃЌ дђЁЯEFB=90ЁуЃЎ ЁпBEЁЭCBЃЌДЙзуЮЊBЃЌЧвBC=BEЃЌЁЯBOC=90ЁуЃЌ
ЁрЁЯCOB=ЁЯEFBЃЌЁЯCBO=ЁЯBEFЃЎ ЁрЁїBCOЁеЁїEBFЃЎ ЁпAЃЈ-4ЃЌ0ЃЉBЃЈ4ЃЌ0ЃЉЃЌCЃЈ-6ЃЌ0ЃЉЃЌ
ЁрEF=OB=4ЃЌBF=OC=6ЃЎ ЁрЕуEЕФзјБъЮЊЃЈ4ЃЌ-2ЃЉЃЎ ЁпAЃЈ-4ЃЌ0ЃЉЃЎ
ЩшЙ§ЕуAЁЂEЕФНтЮіЪНЮЊЃКy=kx+bЃЎ
дђ![]() ЃЎ НтЕУЃЌkЃН
ЃЎ НтЕУЃЌkЃН![]() ЃЌbЃН1ЃЎ ЁрyЃН
ЃЌbЃН1ЃЎ ЁрyЃН![]() x1ЃЎ
x1ЃЎ
Сюx=0ЃЌдђy=-1ЃЎ ЙЪЕуPЕФзјБъЮЊЃЈ0ЃЌ-1ЃЉЃЎ
ЃЈ2ЃЉИљОнЬтвтЃЌЗжСНжжЧщПіЃК
ЕквЛжжЧщПіШчЭМЫљЪОЃК
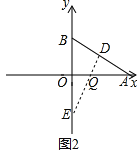
ЁпAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌЁїEOQЁеЁїAOBЃЌ ЁрOQ=OBЃЌOE=OAЃЎ
ЁрAQ=3ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌ-6ЃЉЃЎ ЁпЕуQДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌ
ЁрЕуQдЫЖЏЕФЪБМфt=3УыЃЎ ЙЪДЫЪБtЕФжЕЮЊ3ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌ-6ЃЉЃЎ
ЕкЖўжжЧщПіШчЯТЭМЫљЪОЃК
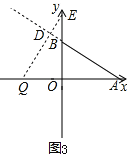
ЁпAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌЁїEOQЁеЁїAOBЃЌ ЁрOQ=OBЃЌOE=OAЃЎ
ЁрAQ=9ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЎ ЁпЕуQДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌ
ЁрЕуQдЫЖЏЕФЪБМфt=9УыЃЎ ЙЪДЫЪБtЕФжЕЮЊ9ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЎ