题目内容
在数学的学习过程中,我们经常用以下的探索过程解决相关问题.
数学问题:三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么可以剪得多少个这样的三角形?
探索规律:为了解决这个问题,我们可以从n=1、n=2、n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
(1)填表:当三角形内有4个点时,把表格补充完整;
(2)你发现的变化规律是: ;
(3)猜想:当三角形内点的个数为n时,最多可以剪得 个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
问题解决:请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
数学问题:三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么可以剪得多少个这样的三角形?
探索规律:为了解决这个问题,我们可以从n=1、n=2、n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
| 三角形内点的个数 | 图形 | 最多剪出的小三解形个数 |
| 1 | 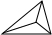 |
3 |
| 2 | 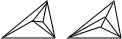 |
5 |
| 3 | 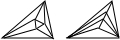 |
7 |
| 4 | ||
| … | … | … |
(2)你发现的变化规律是:
(3)猜想:当三角形内点的个数为n时,最多可以剪得
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
问题解决:请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
考点:规律型:图形的变化类
专题:
分析:(1)根据题意画出图形,进而得出答案;
(2)利用表格中数据得出三角形个数的变化规律即可;
(3)利用(2)中变化规律得出当三角形内点的个数为n时,最多可以剪得三角形的个数,进而利用补项法求出答案.
(2)利用表格中数据得出三角形个数的变化规律即可;
(3)利用(2)中变化规律得出当三角形内点的个数为n时,最多可以剪得三角形的个数,进而利用补项法求出答案.
解答:解:(1)当三角形内有4个点时,把表格补充完整如下:
(2)∵当三角形内点的个数为1时,最多可以剪得3个三角形;
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
当三角形内点的个数为4时,最多可以剪得9个三角形;
∴变化规律是:剪出的三角形个数是连续的奇数;
故答案为:剪出的三角形个数是连续的奇数;
(3)∵1×2+1=3,2×2+1=5,3×2+1=7,
∴当三角形内点的个数为n时,最多可以剪得 2n+1个三角形;
1+3+5+7+…+(2n-1)+(2n+1)
=
[1+3+5+7+…+(2n-1)+(2n+1)][(2n+1)+(2n-1)+…+7+5+3+1]
=
(n+1)(1+2n+1)
=(n+1)2
=n2+2n+1.
| 三角形内点的个数 | 图形 | 最多剪出的小三解形个数 |
| 1 |  |
3 |
| 2 |  |
5 |
| 3 |  |
7 |
| 4 |  |
9 |
| … | … | … |
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
当三角形内点的个数为4时,最多可以剪得9个三角形;
∴变化规律是:剪出的三角形个数是连续的奇数;
故答案为:剪出的三角形个数是连续的奇数;
(3)∵1×2+1=3,2×2+1=5,3×2+1=7,
∴当三角形内点的个数为n时,最多可以剪得 2n+1个三角形;
1+3+5+7+…+(2n-1)+(2n+1)
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=(n+1)2
=n2+2n+1.
点评:此题主要考查了图形变化类,根据题意得出图形中三角形个数变化规律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列等式正确的是( )
| A、a-(b+c)=a-b+c |
| B、a-b+c=a-(b-c) |
| C、a-2(b-c)=a-2b-c |
| D、a-b+c=a-(-b)-(-c) |
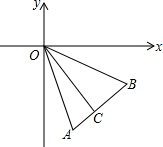 如图,在平面直角坐标系中,A、B两点分别位于第四象限,且∠AOB=45°,OC⊥AB于C,把△AOC沿直线OA翻折后,OC边恰好落在y轴上,若AC=1,OC=3,求经过点A的双曲线和B点坐标.
如图,在平面直角坐标系中,A、B两点分别位于第四象限,且∠AOB=45°,OC⊥AB于C,把△AOC沿直线OA翻折后,OC边恰好落在y轴上,若AC=1,OC=3,求经过点A的双曲线和B点坐标.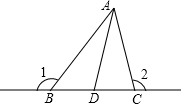 如图,在△ABC中,∠1+∠2=240°,AD平分∠BAC.求∠DAC的度数.
如图,在△ABC中,∠1+∠2=240°,AD平分∠BAC.求∠DAC的度数.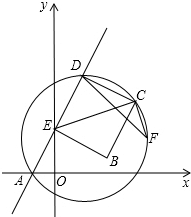 如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是在第一象限内直线上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.
如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是在第一象限内直线上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.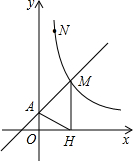 如图,直线y=x+1与y轴交于A点,与反比例函数
如图,直线y=x+1与y轴交于A点,与反比例函数