题目内容
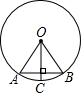如图，在⊙O中，弦AB等于⊙O的半径，OC⊥AB交⊙O于C，则∠ABC=分析：因为OA=OB=AB，从而可知△OAB是等边三角形，则∠AOB=60°，又因为OC⊥AB交⊙O于C，所以∠AOC=30°，则∠ABC=
∠AOC=15°．
| 1 |
| 2 |
解答：解：∵OA=OB=AB
∴△OAB是等边三角形，∠AOB=60°，OC⊥AB交⊙O于C
∴∠AOC=30°
∴∠ABC=
∠AOC=15°．
故答案为：15．
∴△OAB是等边三角形，∠AOB=60°，OC⊥AB交⊙O于C
∴∠AOC=30°
∴∠ABC=
| 1 |
| 2 |
故答案为：15．
点评：本题利用了圆周角定理和垂径定理，等边三角形的判定和性质求解．
练习册系列答案
相关题目
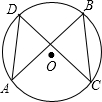已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．