题目内容
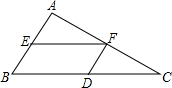 (2013•梧州一模)如图,在△ABC中,AB=6,AC=8,BC=10,点E在边BA上以每秒2个单位的速度由B向A移动,过E作EF∥BC交AC于F,再过F作FD∥AB交BC于D,设E移动的时间为x(秒),EF为 y.
(2013•梧州一模)如图,在△ABC中,AB=6,AC=8,BC=10,点E在边BA上以每秒2个单位的速度由B向A移动,过E作EF∥BC交AC于F,再过F作FD∥AB交BC于D,设E移动的时间为x(秒),EF为 y.(1)求y与x之间的函数关系式.
(2)当x=
| 15 |
| 8 |
| 15 |
| 8 |
(3)设四边形BDFE的面积为S,求S与x之间的函数关系式;并求E在AB边上何处时,四边形BDFE的面积最大?最大面积是多少?
分析:(1)证△AEF∽△ABC,得出比例式,代入求出即可;
(2)根据菱形性质得出BE=EF,代入得出关于x的方程,求出x即可;
(3)求出∠BAC=90°,作EG⊥BD于G,证△ABC∽△GBE,得出
=
,求出EG=
x,根据平行四边形面积公式得出S=
x•(-
x+10),求出函数的最值即可.
(2)根据菱形性质得出BE=EF,代入得出关于x的方程,求出x即可;
(3)求出∠BAC=90°,作EG⊥BD于G,证△ABC∽△GBE,得出
| EG |
| AC |
| BE |
| BC |
| 8 |
| 5 |
| 8 |
| 5 |
| 10 |
| 3 |
解答:解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴
=
,
∴
=
,
∴y=-
x+10;
(2)∵四边形BEFD是菱形,
∴BE=EF,
即2x=-
x+10,
解得:x=
;
(3)在△ABC中,AB=6,AC=8,BC=10,
∴AB2+AC2=BC2,
∴∠BAC=90°,
作EG⊥BD于G,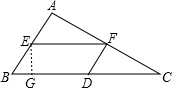
∵在△ABC和△GBE中,∠ABC=∠GBE,∠BAC=∠BGE,
∴△ABC∽△GBE,
∴
=
,
∴
=
,
∴EG=
x,
∴S=
x•(-
x+10)
=-
(x-1.5)2+12,
∴当x=1.5时,S的最大值为12,此时2x=3,
当点E在AB的中点时,四边形BDEF的面积最大,最大面积为12.
故答案为:
.
∴△AEF∽△ABC,
∴
| AE |
| AB |
| EF |
| BC |
∴
| 6-2x |
| 6 |
| y |
| 10 |
∴y=-
| 10 |
| 3 |
(2)∵四边形BEFD是菱形,
∴BE=EF,
即2x=-
| 10 |
| 3 |
解得:x=
| 15 |
| 8 |
(3)在△ABC中,AB=6,AC=8,BC=10,
∴AB2+AC2=BC2,
∴∠BAC=90°,
作EG⊥BD于G,

∵在△ABC和△GBE中,∠ABC=∠GBE,∠BAC=∠BGE,
∴△ABC∽△GBE,
∴
| EG |
| AC |
| BE |
| BC |
∴
| EG |
| 8 |
| 2x |
| 10 |
∴EG=
| 8 |
| 5 |
∴S=
| 8 |
| 5 |
| 10 |
| 3 |
=-
| 16 |
| 3 |
∴当x=1.5时,S的最大值为12,此时2x=3,
当点E在AB的中点时,四边形BDEF的面积最大,最大面积为12.
故答案为:
| 15 |
| 8 |
点评:本题考查了相似三角形的性质和判定,勾股定理的逆定理,二次函数的最值,平行四边形的性质,菱形的性质和判定等知识点的应用,主要考查学生综合运用性质进行计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
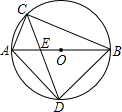 (2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是
(2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是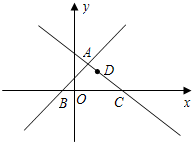 (2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-
(2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=- (2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )
(2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )