题目内容
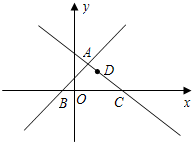 (2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-
(2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-| 3 |
| 4 |
(1)点A,B,C的坐标是A
(
,
)
| 8 |
| 7 |
| 15 |
| 7 |
(
,
)
,B| 8 |
| 7 |
| 15 |
| 7 |
(-1,0)
(-1,0)
,C(4,0)
(4,0)
.(2)当△CBD为等腰三角形时,点D的坐标是
(
,
)或(8,-3)
| 3 |
| 2 |
| 15 |
| 8 |
(
,
)或(8,-3)
.| 3 |
| 2 |
| 15 |
| 8 |
(3)在(2)中,当点D在第四象限时,过点D的反比例函数解析式是
y=-
| 24 |
| x |
y=-
.| 24 |
| x |
分析:(1)先把y=x+1与y=-
x+3联立起来组成方程组,解方程组可得到A点坐标;再把y=0分别代入两函数解析式可确定B点与C点坐标;
(2)分类讨论:当DB=DC,则D点的横坐标为
,然后把x=
代入y=-
x+3可确定D点的纵坐标;当BC=BD=5,设D点坐标为(x、y),然后利用勾股定理建立等量关系求解;
(3)利用待定系数法求反比例解析式.
| 3 |
| 4 |
(2)分类讨论:当DB=DC,则D点的横坐标为
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
(3)利用待定系数法求反比例解析式.
解答:解:(1)解方程组
得
,则点A的坐标为(
,
),
把y=0代入y=x+1得x+1=0,解得x=-1,则B点坐标为(-1,0);
把y=0代入y=-
x+3得-
x+3=0,解得x=4,则C点坐标为(4,0);
(2)当DB=DC时,点D坐标为(
,
);
当BD=CD时,点D的坐标为(8,-3);
(3)设反比例函数解析式为y=
,把D(8,-3)代入得k=-3×8=-24,
所以反比例函数的解析式为y=-
.
故答案为(
,
);(-1,0);(4,0);(
,
)或(8,-3);y=-
.
|
|
| 8 |
| 7 |
| 15 |
| 7 |
把y=0代入y=x+1得x+1=0,解得x=-1,则B点坐标为(-1,0);
把y=0代入y=-
| 3 |
| 4 |
| 3 |
| 4 |
(2)当DB=DC时,点D坐标为(
| 3 |
| 2 |
| 15 |
| 8 |
当BD=CD时,点D的坐标为(8,-3);
(3)设反比例函数解析式为y=
| k |
| x |
所以反比例函数的解析式为y=-
| 24 |
| x |
故答案为(
| 8 |
| 7 |
| 15 |
| 7 |
| 3 |
| 2 |
| 15 |
| 8 |
| 24 |
| x |
点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.

练习册系列答案
相关题目
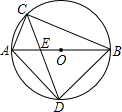 (2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是
(2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是 (2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )
(2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )