题目内容
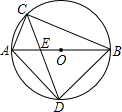 (2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是
(2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是7
| 2 |
7
.| 2 |
分析:根据圆周角定理及勾股定理可得AD的长,过E作EF⊥AC于F,EG⊥BC于G,F,G是垂足,则四边形CFEG是正方形,设EF=EG=x,由三角形面积公式可求出x的值,及CE的值,根据△ADE∽△CBE,根据相似比可求出DE的长,进而求出CD的长.
解答: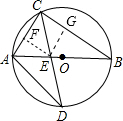 解:∵AB是直径,
解:∵AB是直径,
∴∠ACB=90°,
∵AB=10cm,AC=6cm,
∴BC=
=
=8(cm),
∵CD平分∠ACB,
∴
=
,
∴AD=BD,
∴AD=BD=
AB=5
(cm),
过E作EF⊥AC于F,EG⊥BC于G,F,G是垂足,则四边形CFEG是正方形,
设EF=EG=x,
∴
AC•x+
BC•x=
AC•BC,
∴
×6•x+
×8×x=
×6×8,
∴x=
,
∴CE=
x=
,
∵∠DAB=∠DCB,
∵△ADE∽△CBE,
∴DE:BE=AE:CE=AD:BC,
∴DE:BE=AE:
=5
:8,
∴AE=
,BE=AB-AE=10-
=
,
∴DE=
,
∴CD=CE+DE=
+
=7
(cm).
 解:∵AB是直径,
解:∵AB是直径,∴∠ACB=90°,
∵AB=10cm,AC=6cm,
∴BC=
| AB2-AC2 |
| 102-62 |
∵CD平分∠ACB,
∴
 |
| AD |
 |
| BD |
∴AD=BD,
∴AD=BD=
| ||
| 2 |
| 2 |
过E作EF⊥AC于F,EG⊥BC于G,F,G是垂足,则四边形CFEG是正方形,
设EF=EG=x,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 24 |
| 7 |
∴CE=
| 2 |
| 24 |
| 7 |
| 2 |
∵∠DAB=∠DCB,
∵△ADE∽△CBE,
∴DE:BE=AE:CE=AD:BC,
∴DE:BE=AE:
| 24 |
| 7 |
| 2 |
| 2 |
∴AE=
| 30 |
| 7 |
| 30 |
| 7 |
| 40 |
| 7 |
∴DE=
| 25 |
| 7 |
| 2 |
∴CD=CE+DE=
| 24 |
| 7 |
| 2 |
| 25 |
| 7 |
| 2 |
| 2 |
点评:本题综合考查了圆周角定理,垂径定理,角平分线的性质,及相似三角形的性质.解答此题的关键是作出辅助线,构造正方形.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
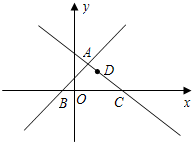 (2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-
(2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=- (2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )
(2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )