题目内容
如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.

(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.

①∵函数的图象与x轴相交于O,
∴0=k+1,
∴k=-1,
∴y=x2-3x,
②假设存在点B,过点B做BD⊥x轴于点D,
∵△AOB的面积等于6,
∴
AO•BD=6,
当0=x2-3x,
x(x-3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2-3x,
解得:x=4或x=-1(舍去).
又∵顶点坐标为:(1.5,-2.25).
∵2.25<4,
∴x轴下方不存在B点,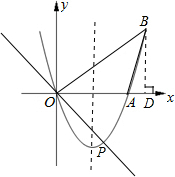
∴点B的坐标为:(4,4);
③∵点B的坐标为:(4,4),
∴∠BOD=45°,BO=
=4
,
当∠POB=90°,
∴∠POD=45°,
设P点横坐标为:x,则纵坐标为:x2-3x,
即-x=x2-3x,
解得x=2或x=0,
∴在抛物线上仅存在一点P(2,-2).
∴OP=
=2
,
使∠POB=90°,
∴△POB的面积为:
PO•BO=
×4
×2
=8.
∴0=k+1,
∴k=-1,
∴y=x2-3x,
②假设存在点B,过点B做BD⊥x轴于点D,
∵△AOB的面积等于6,
∴
| 1 |
| 2 |
当0=x2-3x,
x(x-3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2-3x,
解得:x=4或x=-1(舍去).
又∵顶点坐标为:(1.5,-2.25).
∵2.25<4,
∴x轴下方不存在B点,

∴点B的坐标为:(4,4);
③∵点B的坐标为:(4,4),
∴∠BOD=45°,BO=
| 42+42 |
| 2 |
当∠POB=90°,
∴∠POD=45°,
设P点横坐标为:x,则纵坐标为:x2-3x,
即-x=x2-3x,
解得x=2或x=0,
∴在抛物线上仅存在一点P(2,-2).
∴OP=
| 22+22 |
| 2 |
使∠POB=90°,
∴△POB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x轴的负半轴交于点B,且S△OAB=a.
x轴的负半轴交于点B,且S△OAB=a.
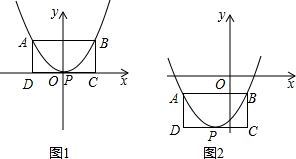 积为常数时,矩形ABCD需要满足什么条件并说明理由.
积为常数时,矩形ABCD需要满足什么条件并说明理由.

 园的面积y(米2)与x(米)的关系式为______.(不要求写出自变量x的取值范围)
园的面积y(米2)与x(米)的关系式为______.(不要求写出自变量x的取值范围)