题目内容
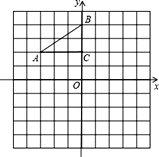
【题目】如图,已知直线![]() 与两坐标轴分别交于A、B两点,抛物线
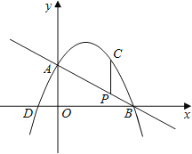
与两坐标轴分别交于A、B两点,抛物线![]() 经过点A、B,点P为直线AB上的一个动点,过P作y轴的平行线与抛物线交于C点, 抛物线与x轴另一个交点为D.
经过点A、B,点P为直线AB上的一个动点,过P作y轴的平行线与抛物线交于C点, 抛物线与x轴另一个交点为D.
(1)求图中抛物线的解析式;
(2)当点P在线段AB上运动时,求线段PC的长度的最大值;
(3)在直线AB上是否存在点P,使得以O、A、P、C为顶点的四边形是平行四边形?若存在,请求出此时点P 的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,线段PC有最大值是2;(3)
时,线段PC有最大值是2;(3)![]() ,
,![]() ,
,![]()
【解析】
把x=0,y=0分别代入解析式可求点A,点B坐标,由待定系数法可求解析式;
设点C![]() ,可求PC
,可求PC![]() ,由二次函数的性质可求解;
,由二次函数的性质可求解;
设点P的坐标为(x,![]() x+2),则点C
x+2),则点C![]() ,分三种情况讨论,由平行四边形的性质可出点P的坐标.
,分三种情况讨论,由平行四边形的性质可出点P的坐标.
解:(1)可求得 A(0,2 ),B(4,0 )
∵抛物线![]() 经过点A和点B
经过点A和点B
∴把(0,2),(4,0)分别代入![]() 得:
得:![]()
解得:![]()
∴抛物线的解析式为![]() .
.
(2)设点P的坐标为(x,![]() x+2),则C(
x+2),则C(![]() )
)

∵点P在线段AB上
∴![]()
∴当![]() 时,线段PC有最大值是2
时,线段PC有最大值是2
(3)设点P的坐标为(x,![]() x+2),
x+2),
∵PC⊥x轴,
∴点C的横坐标为x,又点C在抛物线上,
∴点C(x,![]() )
)
①当点P在第一象限时,假设存在这样的点P,使四边形AOPC为平行四边形,

则OA=PC=2,即![]() ,
,
化简得:![]() ,
,
解得x1=x2=2把x=2代入![]()
则点P的坐标为(2,1)
②当点P在第二象限时,假设存在这样的点P,使四边形AOCP为平行四边形,

则OA=PC=2,即![]() ,
,
化简得:![]() ,
,
解得:![]()
把![]() ,
,
则点P的坐标为![]() ;
;
③当点P在第四象限时,假设存在这样的点P,使四边形AOCP为平行四边形,

则OA=PC=2,即![]() ,
,
化简得:![]() ,
,
解得:![]()
把![]()
则点P的坐标为![]()
综上,使以O、A.P、C为顶点的四边形是平行四边形,
满足的点P的坐标为![]() .
.

 阅读快车系列答案
阅读快车系列答案