Question

【题目】如图，在平面直角坐标系中，菱形OBCD的边OB在x轴上，反比例函数y= （x＞0）的图象经过菱形对角线的交点A，且与边BC交于点F，点A的坐标为（4，2）．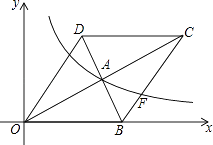

（1）求反比例函数的表达式；
（2）求点F的坐标．

Answer 1

【答案】
（1）解：∵反比例函数y= 的图象经过点A，A点的坐标为（4，2），

∴k=2×4=8，

∴反比例函数的解析式为y=

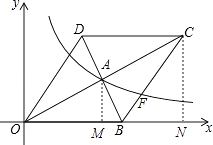
（2）解：过点A作AM⊥x轴于点M，过点C作CN⊥x轴于点N，

由题意可知，CN=2AM=4，ON=2OM=8，

∴点C的坐标为C（8，4），

设OB=x，则BC=x，BN=8﹣x，

在Rt△CNB中，x2﹣（8﹣x）2=42，

解得：x=5，

∴点B的坐标为B（5，0），

设直线BC的函数表达式为y=ax+b，直线BC过点B（5，0），C（8，4），

∴ ，

解得： ，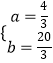

∴直线BC的解析式为y= x+ ，

根据题意得方程组 ，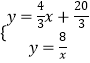

解此方程组得： 或

∵点F在第一象限，

∴点F的坐标为F（6， ）．

【解析】（1）将点A的坐标代入到反比例函数的一般形式后求得k值即可确定函数的解析式；（2）过点A作AM⊥x轴于点M，过点C作CN⊥x轴于点N，首先求得点B的坐标，然后求得直线BC的解析式，求得直线和抛物线的交点坐标即可．本题考查了反比例函数图象上的点的特点、待定系数法确定反比例函数的解析式等知识，解题的关键是能够根据点C的坐标确定点B的坐标，从而确定直线的解析式．
【考点精析】根据题目的已知条件，利用菱形的性质的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．