题目内容
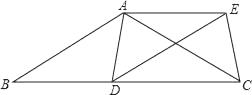
【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.
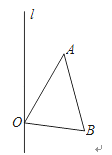
(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
【答案】(1)作图见解析;(2)平行;(3)∠AOC=60°.
【解析】试题分析:(1)根据轴对称的性质画出图形即可;
(2)根据轴对称的性质可直接得出结论;
(3)先根据轴对称图形的性质得出△AOB≌△COD,故可得出∠OBD=∠ODB,∠ABO+∠OBD=∠CDO+∠ODB,即∠ABD=∠CDB,再由∠ABD=2∠ADB可知∠CDB=2∠ADB,故∠CDA=∠ADB,根据AC∥BD,可知∠CAD=∠ADB,∠CAD=∠CDA,所以CA=CD,故可得出AO=OC=AC,即△AOC为等边三角形.
试题解析:(1)如图1所示;

(2)∵AC与BD是对应点的连线,
∴AC∥BD,
故答案为:平行;
(3)如图2,∵由(1)可知,△AOB与△COD关于直线l对称,

∴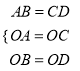 ,
,
∴△AOB≌△COD,
∴∠OBD=∠ODB,
∴∠ABO+∠OBD=∠CDO+∠ODB,即∠ABD=∠CDB,
∵∠ABD=2∠ADB,
∴∠CDB=2∠ADB,
∴∠CDA=∠ADB,
由(2)可知,AC∥BD,∴∠CAD=∠ADB.∴∠CAD=∠CDA,
∴CA=CD,
∵AO=AB,
∴AO=OC=AC,即△AOC为等边三角形,
∴∠AOC=60°.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目