题目内容

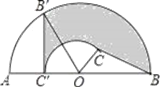
【题目】如图，C为半圆内一点，O为圆心，直径AB长为4cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为______cm2．

【答案】.

【解析】试题分析：已知∠BOC=60°，△B′OC′是△BOC绕圆心O逆时针旋转得到的，可得∠B′OC′=60°，△BCO=△B′C′O，所以∠B′OC=60°，∠C′B′O=30°，即∠B′OB=∠B′OC+∠BOC=120°；又因AB=2cm，可得OB=1cm，OC′=，由此计算出B′C′=，所以阴影部分面积=S扇形B′OB+S△B′C′O﹣S△BCO﹣S扇形C′OC=S扇形B′OB﹣S扇形C′OC=.

练习册系列答案
相关题目

【题目】如图，已知△ABC是等边三角形，点D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：

①△ABE≌△ACF；②BC=DF；③S△ABC=S△ACF+S△DCF；④若BD=2DC，则GF=2EG．其中正确的结论是 ．（填写所有正确结论的序号）

【题目】因式分解：x2﹣36= ．

【题目】如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件：①∠EBO=∠DCO；②BE=CD；③OB=OC．
（1）上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？（用序号写出所有成立的情形）
（2）请选择（1）中的一种情形，写出证明过程．

【题目】如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于______度．

【题目】Rt△ABC与Rt△DEF的位置如图所示，其中AC=2，BC=6，DE=3，∠D=30°，其中，Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动，射线DE、DF与射线AB分别交于N、M两点，运动时间为t，当点E运动到与点B重合时停止运动．

（1）当Rt△DEF在起始时，求∠AMF的度数；

（2）设BC的中点的为P，当△PBM为等腰三角形时，求t的值；

（3）若两个三角形重叠部分的面积为S，写出S与t的函数关系式和相应的自变量的取值范围．

【题目】如图，已知，A（0，4），B（﹣3，0），C（2，0），D为B点关于AC的对称点，反比例函数y= 的图象经过D点．

（1）证明四边形ABCD为菱形；

（2）求此反比例函数的解析式；

（3）已知在y=的图象（x＞0）上一点N，y轴正半轴上一点M，且四边形ABMN是平行四边形，求M点的坐标．

【题目】几何学中，有“点动成_____________，线动成______________，_________________动成体”的原理．

【题目】已知二次函数y＝ax2＋bx＋c中x和y的值如下表：( )

x

0.10

0.11

0.12

0.13

0.14

y

-5.6

-3.1

-1.5

0.9

1.8

则ax2＋bx＋c=0的一个根的范围是( )

A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网