题目内容
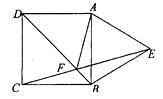
【题目】Rt△ABC与Rt△DEF的位置如图所示，其中AC=2
，BC=6，DE=3
，∠D=30°，其中，Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动，射线DE、DF与射线AB分别交于N、M两点，运动时间为t，当点E运动到与点B重合时停止运动．
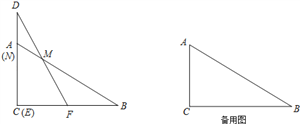
（1）当Rt△DEF在起始时，求∠AMF的度数；
（2）设BC的中点的为P，当△PBM为等腰三角形时，求t的值；
（3）若两个三角形重叠部分的面积为S，写出S与t的函数关系式和相应的自变量的取值范围．
【答案】(1) ∠AMF =150°；(2) t的值为0，3﹣
，2，3+
;(3) S=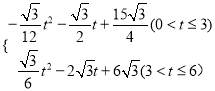
．
【解析】试题分析：（1）根据题意可以求得∠B的度数，∠DFC的度数，从而可以求得∠AME的度数；
（2）根据题意可以分两种情况，一种是DM与线段AB相交，一种是DF与AB的延长线相交，分别针对两种情况再讨论，画出相应的图形，求出相应的t的值；
（3）根据题意可以分两种情况，一种是DM与线段AB相交，一种是DF与AB的延长线相交，然后根据题意可以分别求出两种情况下S与t的函数关系式．
试题解析：（1）在Rt△ABC中，tan∠B=
∴∠B=30°，
在Rt△DEF中，∠D=30°，
∴∠DFC=60°，
∴∠FMB=∠DFC﹣∠B=30°，
∴∠AMF=180°﹣∠FMB=150°；
（2）∵BC=6，点P为线段BC的中点，
∴BP=3，
（ⅰ）若点M在线段AB上，
①当PB=PM时，PB=PM=3，
∵DE=3
，∠D=30°，
∴EF=DEtan30°=3，
∴此时t=0；
②如图（1）所示
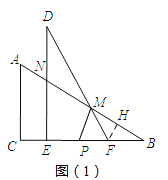
当BP=BM时，BP=BM=3，
∵∠B=30°，∠DFE=60°，
∴∠FMB=30°，
∴△BMF为等腰三角形．
过点F作FH⊥MB于H，则BH=
BM=
，
在Rt△BHF中，∠B=30°，
∴BF=
，
∴t=3﹣
；
③如图（2）所示，
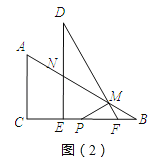
当MP=MB时，∠MPB=∠B=30
∵∠MFP=60°，
∴PM⊥MF，∠BMF=30°
∴FB=FM，
设FB=x，则FM=x，PF=2x．
∴3x=3，x=1
∴t=2；
（ⅱ）若点M在射线AB上，如图（3）所示，
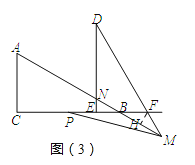
∵∠PBM=150°
∴当△PBM为等腰三角形时，有BP=BM=3
∵△BFM为等腰三角形，
∴过点F作FH⊥BM于H，则BH=
BM=
，
在Rt△BHF中，∠FBH=30°
∴BF=
，
∴t=3+
，
综上所述，t的值为0，3﹣
，2，3+
．
（3）当0＜t≤3时，BE=6﹣t，NE=
（6﹣t），
∴SΔBEN=
×(6-t) ×
（6﹣t）=
（6﹣t）2
过点F作FH⊥MB于H，如图（1）所示，
∵FB=3﹣t
∴HF=
（3﹣t），HB=
（3﹣t），MB=
（3﹣t），
∴SΔBMF=
×
（3﹣t）×
（3﹣t）=
（3﹣t）2，
∴S=S△BEN﹣S△BMF=
（6﹣t）2-
（3﹣t）2=
当3＜t≤6时，BE=6﹣t，NE=
（6﹣t），如图（4）所示，
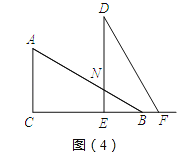
∴S=SΔBEN=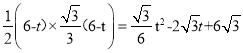
由上可得，当0＜t≤3时，S=
，
当3＜t≤6时，S=
．
