题目内容
【题目】如图,等腰三角形ABC内接于⊙O,CA=CB,过点A作AE∥BC,交⊙O于点E,过点C作⊙O的切线交AE的延长线于点D,已知AB=6,BE=3![]() .
.
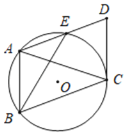
(1)求证:四边形ABCD为平行四边形;
(2)延长AO交DC的延长线于点F,求AF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由题意连接CO并延长交AB于H,如图1,利用切线的性质得OC⊥DC,再证明CO为AB的中垂线,则CO⊥AB,所以AB∥CD,然后根据平行四边形的判定方法得到结论;
(2)根据题意利用平行线的性质得到∠DAC=∠BCA,则![]() =
=![]() ,所以
,所以![]() =
=![]() ,于是得到CB=CA=BE=3
,于是得到CB=CA=BE=3![]() ,利用垂径定理得到AH=3,则根据勾股定理可计算出CH=9,设⊙O的半径为r,则OH=9﹣r,在Rt△OAH中利用(9﹣r)2+32=r2得r=5,然后证明△AOH~△FOC,利用相似比求出OF,从而得到AF的长.
,利用垂径定理得到AH=3,则根据勾股定理可计算出CH=9,设⊙O的半径为r,则OH=9﹣r,在Rt△OAH中利用(9﹣r)2+32=r2得r=5,然后证明△AOH~△FOC,利用相似比求出OF,从而得到AF的长.
解:(1)证明:连接CO并延长交AB于H,如图1,
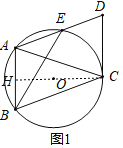
∵CD与⊙O相切于点C,
∴OC⊥DC,
∵OA=OB,CA=CB,
∴CO为AB的中垂线,
∴CO⊥AB,
∴AB∥CD,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:如图2,
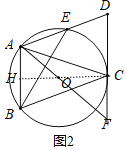
∵AD∥BC,
∴∠DAC=∠BCA,
∴![]() =
=![]() ,
,
∵![]() ,即
,即![]() =
=![]() ,
,
∴CB=CA=BE=3![]() ,
,
∵CH⊥AB,
∴AH=BH=![]() AB=3,
AB=3,
在Rt△ACH中,CH=![]() =9,
=9,
设⊙O的半径为r,则OH=9﹣r,
在Rt△OAH中,(9﹣r)2+32=r2,解得r=5,
∴OH=4,
∵AH∥CF,
∴△AOH~△FOC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得OF=![]() ,
,
∴AF=AO+OF=5+![]() =
=![]() .
.

【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋中并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | _____ | _____ | _____ |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个黑球的概率是______.(结果都保留小数点后两位)
(2)估算袋中白球的个数为________.
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算出两次都摸出白球的概率.
【题目】某校为了解学生的课外阅读情况,随机调查了部分学生平均每天的课外阅读时间,并根据调查结果制成被调查学生人数的统计图表如下,但信息不完整.
时间(小时) | 0.5 | 1 | 1.5 | 2 |
人数 | 2 | 5 | 3 |
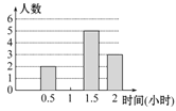
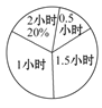
请根据所提供信息,解决下列问题:
(1)求扇形统计图中,读书时间为“2小时”部分的圆心角的度数.
(2)通过计算估计全校每个学生平均每天的课外阅读时间.
(3)从被调查的课外读书时间最少和最多的学生中,随机抽2个学生进行访谈,求各抽到1人的概率.