ƒøƒ⁄»ð
°æƒø°øƒ≥–£Œ™¡ÀΩ‚—ß…˙µƒøŒÕ‚‘ƒ∂¡«Èøˆ£¨Àʪ˙µ˜≤È¡À≤ø∑÷—ß…˙∆Ωæ˘√øÃϵƒøŒÕ‚‘ƒ∂¡ ±º‰£¨≤¢∏˘æðµ˜≤ÈΩ·π˚÷∆≥…±ªµ˜≤È—ß…˙»À ˝µƒÕ≥º∆Õº±Ì»Áœ¬£¨µ´–≈œ¢≤ªÕÍ’˚£Æ
±º‰(–° ±) | 0.5 | 1 | 1.5 | 2 |
»À ˝ | 2 | 5 | 3 |
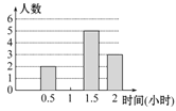
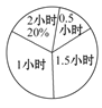
«Î∏˘æðÀ˘Ã·π©–≈œ¢£¨Ω‚戜¬¡–Œ £∫
£®1£©«Û…»–ŒÕ≥º∆Õº÷–£¨∂¡ È ±º‰Œ™°∞2–° ±°±≤ø∑÷µƒ‘≤–ƒΩ«µƒ∂» ˝£Æ
£®2£©Õ®π˝º∆À„π¿º∆»´–£√ø∏ˆ—ß…˙∆Ωæ˘√øÃϵƒøŒÕ‚‘ƒ∂¡ ±º‰£Æ
£®3£©¥”±ªµ˜≤ȵƒøŒÕ‚∂¡ È ±º‰◊Ó…Ÿ∫Õ◊Ó∂ýµƒ—ß…˙÷–£¨Àʪ˙≥È2∏ˆ—ß…˙Ω¯––∑√Ã∏£¨«Û∏˜≥ȵΩ1»Àµƒ∏≈¬ £Æ
°æ¥∞∏°ø£®1£©72°„£ª£®2£©1.3–° ±£ª£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©”√360°„≥À“‘‘ƒ∂¡ ±º‰Œ™2–° ±µƒ≤ø∑÷À˘’ºµƒ±»¿˝º¥ø…£Æ
£®2£©œ»«Û≥ˆ±ªµ˜≤È—ß…˙»À ˝£¨‘Ÿ«Û≥ˆ‘ƒ∂¡ ±º‰Œ™1–° ±µƒ»À ˝£¨º¥ø…«Û≥ˆ±ªµ˜≤È—ß…˙µƒøŒÕ‚‘ƒ∂¡ ±º‰£¨æð¥Àπ¿º∆ø…»´–£√ø∏ˆ—ß…˙∆Ωæ˘√øÃϵƒøŒÕ‚‘ƒ∂¡ ±º‰£Æ
£®3£©”√¡–±Ì«Û≥ˆ“ªπ≤”–∂ý…Ÿ÷÷µ»ø…ƒÐµƒΩ·π˚£¨ø¥∏˜≥ȵΩ1»À”–º∏÷÷Ω·π˚£¨º¥ø…»∑∂®∏˜≥ȵΩ1»Àµƒ∏≈¬ £Æ
£®1£©°þ‘ƒ∂¡ ±º‰Œ™2–° ±µƒ»À ˝’º20%£¨
°ý∆‰‘≤–ƒΩ«Œ™360°„°¡20%=72°„£Æ
£®2£©°þ‘ƒ∂¡ ±º‰Œ™2–° ±µƒ»À ˝Œ™3»À£¨’º20%£¨
°ý±ªµ˜≤È—ß…˙»À ˝Œ™![]() =15£¨
=15£¨
°ý‘ƒ∂¡ ±º‰Œ™1–° ±µƒ»À ˝Œ™15-(2+5+3)=5£¨‘Ú√ø∏ˆ—ß…˙øŒÕ‚∆Ωæ˘‘ƒ∂¡ ±º‰Œ™£∫
![]() (–° ±)
(–° ±)
°ýπ¿º∆»´–£√ø∏ˆ—ß…˙∆Ωæ˘√øÃϵƒøŒÕ‚‘ƒ∂¡ ±º‰Œ™1.3–° ±£Æ
£®3£©…Ë‘ƒ∂¡ ±º‰◊Ó…Ÿµƒ2»ÀŒ™A1£¨A2£¨‘ƒ∂¡ ±º‰◊Ó∂ýµƒ3»ÀŒ™B1£¨B2£¨B3£¨¡–±ÌŒ™£∫
µ⁄∂˛∏ˆ»À µ⁄“ª∏ˆ»À | A1 | A2 | B1 | B2 | B3 |
A1 | ®D | (A1A2) | (A1B1) | (A1B2) | (A1B3) |
A2 | (A2A1) | ®D | (A2B1) | (A2B2) | (A2B3) |
B1 | (B1A1) | (B1A2) | ®D | (B1B2) | (B1B3) |
B2 | (B2A1) | (B2A2) | (B2B1) | ®D | (B2B3) |
B3 | (B3A1) | (B3A2) | (B3B1) | (B3B2) | ®D |
π≤”–20÷÷µ»ø…ƒÐµƒΩ·π˚£¨∆‰÷–∏˜≥ȵΩ1»Àµƒ≥È∑®”–12÷÷£¨‘Ú∏˜≥ȵΩ1»Àµƒ∏≈¬ ![]() £Æ
£Æ

 ∂·π⁄ΩæÌ»´ƒÐ¡∑øºœµ¡–¥∞∏
∂·π⁄ΩæÌ»´ƒÐ¡∑øºœµ¡–¥∞∏