Question

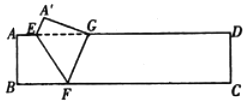
【题目】如图，一张矩形纸片的长AD=12，宽AB=2，点E在边AD上，点F在边BC上，将四边形ABFE沿直线EF翻折后，点B落在边AD的三等分点G处，则EG的长为_______.

Answer 1

【答案】或

【解析】

如图，作GH⊥BC于H．则四边形ABHG是矩形．G是AD的三等分点，推出AG=4或8，证明EG=FG=FB，设EG=FG=FB=x，分两种情形构建方程即可解决问题．

解：如图，作GH⊥BC于H．则四边形ABHG是矩形．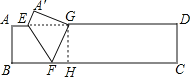

∵G是AD的三等分点，
∴AG=4或8，
由翻折可知：FG=FB，∠EFB=∠EFG，设FG=FB=x．
∵AD∥BC，
∴∠FEG=∠EFB=∠GFE，
∴EG=FG=x，
在Rt△FGH中，∵FG2=GH2+FH2，
∴x2=22+（4-x）2或x2=22+（8-x）2
解得：x=或，
故答案为或．