题目内容
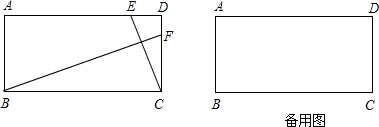
已知在矩形ABCD中,AB=3,AD=6,经过点A把矩形分成两部分,一是直角梯形,一是直角三角形,若梯形的面积与直角三角形的面积之比为3:1,则梯形的周长与直角三角形的周长之比为
- A.
 或
或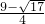
- B.
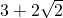 或
或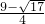
- C.
 或
或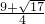
- D.
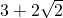 或
或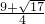
A
分析:根据题目的要求正确地作出图形,首先利用面积之间的关系得到线段BE的长,然后利用勾股定理求得线段AE的长,再求出周长,作比即可.
解答: 解:①如图:设BE=x,则CE=6-x,
解:①如图:设BE=x,则CE=6-x,
∵梯形的面积与直角三角形的面积之比为3:1,
∴ :
: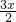 =3:1
=3:1
解得:x=3,
∴AE=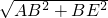 =
=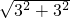 =3
=3 ,
,
∴L梯形:L直角三角形=(6+3+3+3 ):(3+3+3
):(3+3+3 )=3-
)=3- ;
;
②如图1,设DE=x,则CE=3-x,
∵梯形的面积与直角三角形的面积之比为3:1,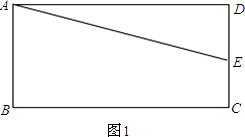
∴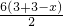 :
: =3:1
=3:1
解得:x= ,
,
∴ =
=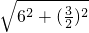 =3
=3 ,
,
∴L梯形:L直角三角形=(3+6+ +3
+3 ):(6+
):(6+ +3
+3 )=
)=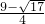 .
.
故选A.
点评:本题考查了矩形的性质及勾股定理,解题的关键是根据不同的情况分类讨论,此类题目是中考中的一个高频考点.
分析:根据题目的要求正确地作出图形,首先利用面积之间的关系得到线段BE的长,然后利用勾股定理求得线段AE的长,再求出周长,作比即可.
解答:
 解:①如图:设BE=x,则CE=6-x,
解:①如图:设BE=x,则CE=6-x,∵梯形的面积与直角三角形的面积之比为3:1,
∴
 :
: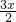 =3:1
=3:1解得:x=3,
∴AE=
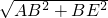 =
=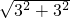 =3
=3 ,
,∴L梯形:L直角三角形=(6+3+3+3
 ):(3+3+3
):(3+3+3 )=3-
)=3- ;
;②如图1,设DE=x,则CE=3-x,
∵梯形的面积与直角三角形的面积之比为3:1,

∴
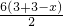 :
: =3:1
=3:1解得:x=
 ,
,∴
 =
=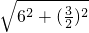 =3
=3 ,
,∴L梯形:L直角三角形=(3+6+
 +3
+3 ):(6+
):(6+ +3
+3 )=
)=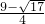 .
.故选A.
点评:本题考查了矩形的性质及勾股定理,解题的关键是根据不同的情况分类讨论,此类题目是中考中的一个高频考点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
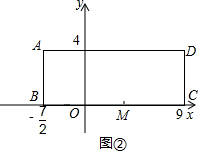
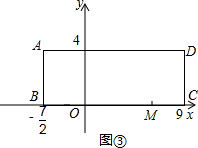
 ,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).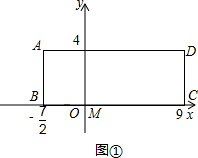
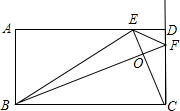
 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.