题目内容
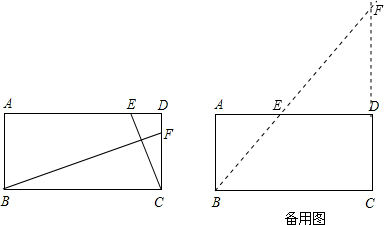
如图,已知在矩形ABCD中,AD=8cm,CD=4cm,点E从点D出发,沿线段DA以每秒1cm的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2cm的速度移动,当B、E、F三点共线时,两点同时停止运动.设点E移动的时间为t(秒),
(1)求证:△BCF∽△CDE;
(2)求t的取值范围;
(3)连接BE,当t为何值时,∠BEC=∠BFC?

(1)求证:△BCF∽△CDE;
(2)求t的取值范围;
(3)连接BE,当t为何值时,∠BEC=∠BFC?
分析:(1)根据矩形的性质和相似三角形的判定方法:两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似,即可证明△BCF∽△CDE;
(2)因为当B、E、F三点共线时,两点同时停止运动,所以可用t表示出此时的DE,BCFD,FC的长,利用相似三角形的性质即可求出t的最大值,进而求出t的取值范围;
(3)因为△BCF∽△CDE利用相似的性质和矩形的性质可证明BC=BE,利用勾股定理即可求出AE的长,进而求出DE的长,时间t也可求出了.
(2)因为当B、E、F三点共线时,两点同时停止运动,所以可用t表示出此时的DE,BCFD,FC的长,利用相似三角形的性质即可求出t的最大值,进而求出t的取值范围;
(3)因为△BCF∽△CDE利用相似的性质和矩形的性质可证明BC=BE,利用勾股定理即可求出AE的长,进而求出DE的长,时间t也可求出了.
解答:解:(1)∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,
∵ED=t,FC=2t,
∴
=
,
∵AD=8cm,CD=4cm,
∴
=
,
∴
=
,
∴△BCF∽△CDE;
(2)已知如图:
∵AD∥BC,
∴△FED∽FBC,
∴
=
,
∴
=
,
∴t=4,
∴0≤t≤4;
(3)∵△BCF∽△CDE,
∴∠DEC=∠BFC
∵AD∥BC,∠DEC=∠ECB,
∴∠BFC=∠ECB,
∵∠BEC=∠BFC,
∴∠BEC=∠ECB,
∴BC=BE,
∵BC=8cm,
∴AB=4cm,∠A=90°,
∴AE=
=4
cm,
∴DE=(8-4
)cm,
∵8-4
<4,
∴t=(8-4
)秒.
∴∠D=∠BCD=90°,
∵ED=t,FC=2t,
∴
| ED |
| FC |
| 1 |
| 2 |
∵AD=8cm,CD=4cm,
∴
| DC |
| BC |
| 1 |
| 2 |
∴
| ED |
| FC |
| DC |
| BC |
∴△BCF∽△CDE;
(2)已知如图:
∵AD∥BC,
∴△FED∽FBC,
∴
| ED |
| BC |
| FD |
| FC |

∴
| t |
| 8 |
| 2t-4 |
| 2t |
∴t=4,
∴0≤t≤4;
(3)∵△BCF∽△CDE,
∴∠DEC=∠BFC
∵AD∥BC,∠DEC=∠ECB,
∴∠BFC=∠ECB,
∵∠BEC=∠BFC,
∴∠BEC=∠ECB,
∴BC=BE,
∵BC=8cm,
∴AB=4cm,∠A=90°,
∴AE=
| BE2-AB2 |
| 3 |
∴DE=(8-4
| 3 |
∵8-4
| 3 |
∴t=(8-4
| 3 |
点评:本题综合性的考查了矩形的性质、相似三角形的判定以及性质、等腰三角形的判定和等腰三角形的性质和勾股定理的运用,题目的难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 自选题:
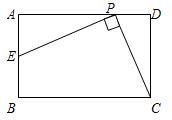
自选题: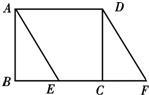 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.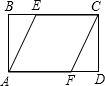 如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积. 如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=
如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=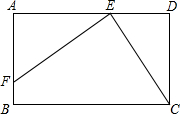 E=3cm,BC=7cm.
E=3cm,BC=7cm.