题目内容
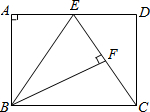 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.求证:△ABE≌△FBE.
分析:根据矩形性质得出AD∥BC,∠A=90°,根据平行线性质和等腰三角形性质得出∠AEB=∠EBC=∠CEB,根据AAS证明两三角形全等即可.
解答:证明:在矩形ABCD中,AD∥BC,∠A=90°,
∵AD∥BC,
∴∠AEB=∠EBC,
∵BC=CE,
∴∠EBC=∠BEC,
∴∠AEB=∠BEC,
∵BF⊥CE,
∴∠A=∠BFE=90°,
在△ABE和△FBE中
∵
,
∴△ABE≌△FBE(AAS).
∵AD∥BC,
∴∠AEB=∠EBC,
∵BC=CE,
∴∠EBC=∠BEC,
∴∠AEB=∠BEC,
∵BF⊥CE,
∴∠A=∠BFE=90°,
在△ABE和△FBE中
∵
|
∴△ABE≌△FBE(AAS).
点评:本题考查了矩形性质、等腰三角形性质、平行线的性质、全等三角形的判定等知识点,主要考查学生的推理能力,题目比较典型,难度适中.

练习册系列答案
相关题目
 (2012•德庆县一模)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE的长度为( )
(2012•德庆县一模)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE的长度为( )