题目内容
已知在矩形ABCD中,AC=12,∠ACB=15°,那么顶点D到AC的距离为分析:先利用三角函数的值分别求出AB及BC,然后利用三角形ADC面积的两种表示形式可求出DE的长.
解答: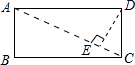 解:由题意得:AB=ACsin∠ACB=3
解:由题意得:AB=ACsin∠ACB=3
-3
,BC=3
+3
,
S△ADC=
AD•DC=
AC•DE=9,
∴DE=3.
故答案为:3.
 解:由题意得:AB=ACsin∠ACB=3
解:由题意得:AB=ACsin∠ACB=3| 6 |
| 2 |
| 6 |
| 2 |
S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=3.
故答案为:3.
点评:此题考查的是矩形的性质,解答本题的关键是根据∠ACB的度数求出AB及AC的长,这要求我们熟练掌握三角函数值的求解方法,必要的时候要借助计算器.

练习册系列答案
相关题目
 ,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).

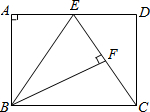 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.