题目内容
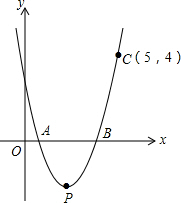如图，抛物线y=ax2-5x+4a与x轴相交于点A、B，且过点C（5，4）．
（1）求点A和点B的坐标；
（2）求a的值和该抛物线顶点P的坐标；
（3）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．
解：（1）∵抛物线y=ax2-5x+4a过点C（5，4），
∴25a-5×5+4a=4，
解得a=1，
∴抛物线解析式为y=x2-5x+4，
令y=0，则x2-5x+4=0，
解得x1=1，x2=4，
所以，点A（1，0），B（4，0）；
（2）由（1）可知，a=1，
又∵y=x2-5x+4=（x-
）2-
，
∴顶点P（，-）；
（3）要使平移后抛物线的顶点落在第二象限，可以先向左平移3个单位，再向上平移3个单位，
平移后的抛物线解析式为y=（x-+3）2-+3=（x+
）2+
=x2+x+
+=x2+x+1，
即y=x2+x+1（答案不唯一）．
分析：（1）把点C的坐标代入抛物线解析式求出a的值，从而得到抛物线解析式，然后令y=0，解关于x的一元二次方程即可得到A、B的坐标；
（2）把抛物线解析式整理成顶点式形式，即可写出顶点P的坐标；
（3）根据平移变换只改变图形的位置，不改变图形的形状与大小，根据点的平移，把顶点平移为第二象限的点即可．
点评：本题二次函数的综合题型，主要考查了待定系数法求二次函数解析式，抛物线与x轴的交点的求解，抛物线顶点坐标的求解，以及抛物线的平移，简单综合题，难度不大，把点C的坐标代入抛物线解析式求出a的值是解题的关键．
∴25a-5×5+4a=4，
解得a=1，
∴抛物线解析式为y=x2-5x+4，
令y=0，则x2-5x+4=0，
解得x1=1，x2=4，
所以，点A（1，0），B（4，0）；
（2）由（1）可知，a=1，
又∵y=x2-5x+4=（x-
）2-，∴顶点P（
，-）；（3）要使平移后抛物线的顶点落在第二象限，可以先向左平移3个单位，再向上平移3个单位，
平移后的抛物线解析式为y=（x-
+3）2-+3=（x+）2+=x2+x++=x2+x+1，即y=x2+x+1（答案不唯一）．
分析：（1）把点C的坐标代入抛物线解析式求出a的值，从而得到抛物线解析式，然后令y=0，解关于x的一元二次方程即可得到A、B的坐标；
（2）把抛物线解析式整理成顶点式形式，即可写出顶点P的坐标；
（3）根据平移变换只改变图形的位置，不改变图形的形状与大小，根据点的平移，把顶点平移为第二象限的点即可．
点评：本题二次函数的综合题型，主要考查了待定系数法求二次函数解析式，抛物线与x轴的交点的求解，抛物线顶点坐标的求解，以及抛物线的平移，简单综合题，难度不大，把点C的坐标代入抛物线解析式求出a的值是解题的关键．
练习册系列答案
相关题目
两点，试问当x为何值时，线段CD有最大值，其最大值为多少？
O为坐标原点，抛物线上一点C的横坐标为1．
此抛物线上，矩形面积为12，
与x轴交于点A、B，点A的坐标为（-2，0）．