题目内容
如图,抛物线y1=-ax2-ax+1经过点P(-| 1 |
| 2 |
| 9 |
| 8 |
(1)求a值;
(2)设y1=-ax2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
分析:(1)抛物线y1=-ax2-ax+1经过点P(-
,
),则把P点的坐标代入解析式就可以求出A的值.
(2)求出A的值以后,两个函数的解析式就可以求出,在解析式中,令y=0就可以求出函数与x轴的交点坐标,得出M,N,E,F四点的坐标.
(3)线段CD的长度可以用x表示出来,即y2与y1的差.CD的长度就可以表示为x的一个二次函数,求CD的最值,就是求函数的最值问题.
| 1 |
| 2 |
| 9 |
| 8 |
(2)求出A的值以后,两个函数的解析式就可以求出,在解析式中,令y=0就可以求出函数与x轴的交点坐标,得出M,N,E,F四点的坐标.
(3)线段CD的长度可以用x表示出来,即y2与y1的差.CD的长度就可以表示为x的一个二次函数,求CD的最值,就是求函数的最值问题.
解答:解:(1)∵点P(-
,
)在抛物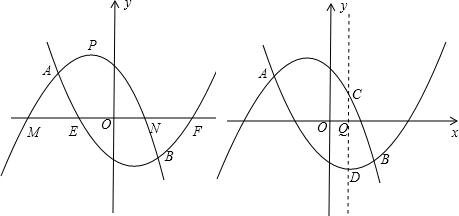
y1=-ax2-ax+1上,
∴-
a+
a+1=
,(2分)
解得a=
.(3分)
(2)如图,由(1)知a=
,
∴抛物线y1=-
x2-
x+1,y2=
x2-
x-1.(5分)
当-
x2-
x+1=0时,解得x1=-2,x2=1.
∵点M在点N的左边,
∴xM=-2,xN=1.(6分)
当
x2-
x-1=0时,解得x3=-1,x4=2.
∵点E在点F的左边,
∴xE=-1,xF=2.(7分)
∵xM+xF=0,xN+xE=0,
∴点M与点F对称,点N与点E对称.(8分)
(3)∵a=
>0.
∴抛物线y1开口向下,抛物线y2开口向上.(9分)
根据题意,得CD=y1-y2=(-
x2-
x+1)-(
x2-
x-1)=-x2+2.(11分)
∵xA≤x≤xB,
∴当x=0时,CD有最大值2.(12分)
| 1 |
| 2 |
| 9 |
| 8 |

y1=-ax2-ax+1上,
∴-
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 8 |
解得a=
| 1 |
| 2 |
(2)如图,由(1)知a=
| 1 |
| 2 |
∴抛物线y1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 1 |
| 2 |
∵点M在点N的左边,
∴xM=-2,xN=1.(6分)
当
| 1 |
| 2 |
| 1 |
| 2 |
∵点E在点F的左边,
∴xE=-1,xF=2.(7分)
∵xM+xF=0,xN+xE=0,
∴点M与点F对称,点N与点E对称.(8分)
(3)∵a=
| 1 |
| 2 |
∴抛物线y1开口向下,抛物线y2开口向上.(9分)
根据题意,得CD=y1-y2=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵xA≤x≤xB,
∴当x=0时,CD有最大值2.(12分)
点评:本题主要考查了函数解析式与图象的关系,在函数图象上的点的坐标一定满足函数的解析式.求最值的问题解决的基本思路是转化为函数求最值的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,则图中阴影部分的面积是( )
如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,则图中阴影部分的面积是( ) 存在,请直接写出Q点坐标;若不存在,请说明理由.
存在,请直接写出Q点坐标;若不存在,请说明理由. (2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
(2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C. 如图,抛物线
如图,抛物线