题目内容
【题目】如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．
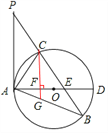
(1)求证：PA是⊙O的切线；
(2)过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AGAB=48，求AC的长；
(3)在满足(2)的条件下，若AF：FD=1：2，GF=2，求⊙O的半径及sin∠ACE的值．
【答案】（1）证明见解析;（2）AC=
;（3）⊙O半径为6,sin∠ACE=
.
【解析】分析:（1）根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案；
（2）首先得出△CAG∽△BAC，进而得出
，求出AC即可；
（3）先求出AF的长，根据勾股定理得： 
，即可得出sin∠ADB=
，利用∠ACE=∠ACB=∠ADB，求出即可．
本题解析：（1）证明：连接CD，
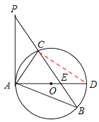
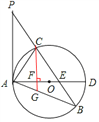
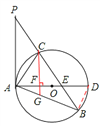
∵AD是⊙O的直径，∴∠ACD=90° ∴∠CAD+∠ADC=90°。
又∵∠PAC=∠PBA，∠ADC=∠PBA， ∴∠PAC=∠ADC。∴∠CAD+∠PAC=90° ∴PA⊥OA。
又∵AD是⊙O的直径，∴PA是⊙O的切线。
（2）由（1）知，PA⊥AD，又∵CF⊥AD，∴CF∥PA。∴∠GCA=∠PAC。
又∵∠PAC=∠PBA，∴∠GCA=∠PBA。
又∵∠CAG=∠BAC，∴△CAG∽△BAC。 ∴
，即AC2=AGAB。
∵AGAB=12，∴AC2=48。∴AC=
。
（3）设AF=x， ∵AF：FD=1：2，∴FD=2x。∴AD=AF+FD=3x。
在Rt△ACD中，∵CF⊥AD，∴AC2=AFAD，即3x2=48。
解得；x=4。 ∴AF=4，AD=12。∴⊙O半径为6。
在Rt△AFG中，∵AF=4，GF=2，
∴根据勾股定理得： 
由（2）知，AGAB=48 
连接BD，∵AD是⊙O的直径，∴∠ABD=90°。
在Rt△ABD中，∵sin∠ADB=
，AD=12， 
∴sin∠ADB=
。
∵∠ACE=∠ACB=∠ADB，∴sin∠ACE=
.
