题目内容
(2012•绍兴模拟)如图所示,P是边长为1的正三角形ABC的BC边上一点,从P向AB作垂线PQ,Q为垂足.延长QP与AC的延长线交于R,设BP=x(0≤x≤1),△BPQ与△CPR的面积之和为y,把y表示为x的函数是 .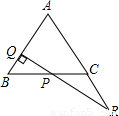
【答案】分析:根据三角函数分别表示出BQ,QP,PC的长,就可以求得△BPQ与△CPR的面积,进而求出函数解析式.
解答: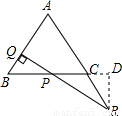 解:∵BP=x,∠B=60°,∠PQB=90°,
解:∵BP=x,∠B=60°,∠PQB=90°,
∴BQ= x,QP=
x,QP=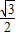 x,PC=1-x.
x,PC=1-x.
∴△BPQ的面积= ×BQ×QP=
×BQ×QP=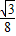 x2,那么AQ=1-
x2,那么AQ=1- x,可得到QR=
x,可得到QR=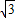 -
-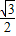 x,
x,
则PR=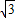 -
-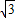 x.
x.
过点R做RD⊥PC,则RD=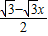 ,
,
∴△CPR的面积= ×PC×RD=
×PC×RD=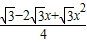 .
.
∵△BPQ与△CPR的面积之和为y,
∴y=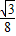 (3x2-4x+2)=
(3x2-4x+2)=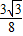 x2-
x2-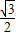 x+
x+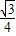 ,
,
∴y=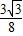 x2-
x2-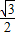 x+
x+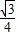 .
.
点评:解决本题的关键是根据所给条件利用三角函数得到相应的三角形的各边的长.
解答:
 解:∵BP=x,∠B=60°,∠PQB=90°,
解:∵BP=x,∠B=60°,∠PQB=90°,∴BQ=
 x,QP=
x,QP=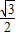 x,PC=1-x.
x,PC=1-x.∴△BPQ的面积=
 ×BQ×QP=
×BQ×QP=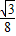 x2,那么AQ=1-
x2,那么AQ=1- x,可得到QR=
x,可得到QR=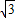 -
-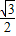 x,
x,则PR=
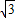 -
-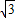 x.
x.过点R做RD⊥PC,则RD=
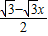 ,
,∴△CPR的面积=
 ×PC×RD=
×PC×RD=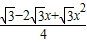 .
.∵△BPQ与△CPR的面积之和为y,
∴y=
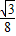 (3x2-4x+2)=
(3x2-4x+2)=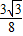 x2-
x2-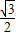 x+
x+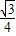 ,
,∴y=
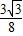 x2-
x2-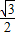 x+
x+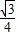 .
.点评:解决本题的关键是根据所给条件利用三角函数得到相应的三角形的各边的长.

练习册系列答案
相关题目
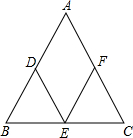 (2012•绍兴模拟)如图,在△ABC中,AB=AC,D、E、F分别是三角形三边中点,试判断四边形ADEF的形状并加以说明.
(2012•绍兴模拟)如图,在△ABC中,AB=AC,D、E、F分别是三角形三边中点,试判断四边形ADEF的形状并加以说明.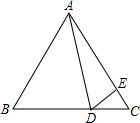 (2012•绍兴模拟)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,CD=3,CE=2.则AE的长等于( )
(2012•绍兴模拟)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,CD=3,CE=2.则AE的长等于( )