题目内容
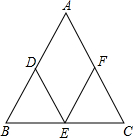 (2012•绍兴模拟)如图,在△ABC中,AB=AC,D、E、F分别是三角形三边中点,试判断四边形ADEF的形状并加以说明.
(2012•绍兴模拟)如图,在△ABC中,AB=AC,D、E、F分别是三角形三边中点,试判断四边形ADEF的形状并加以说明.分析:因为D、E、F分别是AB、BC、AC边上的中点,所以EF∥AB,DE∥AC,根据两组对边分别平行的四边形是平行四边形判定;又因为四边形ADEF是平行四边形,可根据菱形的定义“一组邻边相等的平行四边形是菱形”,证明四边形的邻边相等即可.
解答:证明:∵D、E、F分别是AB、BC、AC的中点,
∴EF∥AB,DE∥AC,
∴四边形ADEF是平行四边形,
∴EF=
AB,DE=
AC,且AB=BC,
∴DE=EF
∴四边形ADEF是菱形.
∴EF∥AB,DE∥AC,
∴四边形ADEF是平行四边形,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=EF
∴四边形ADEF是菱形.
点评:本题考查平行四边形的判定和菱形的判定方法.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
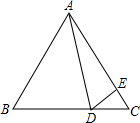 (2012•绍兴模拟)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,CD=3,CE=2.则AE的长等于( )
(2012•绍兴模拟)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,CD=3,CE=2.则AE的长等于( )